Industry Data
-
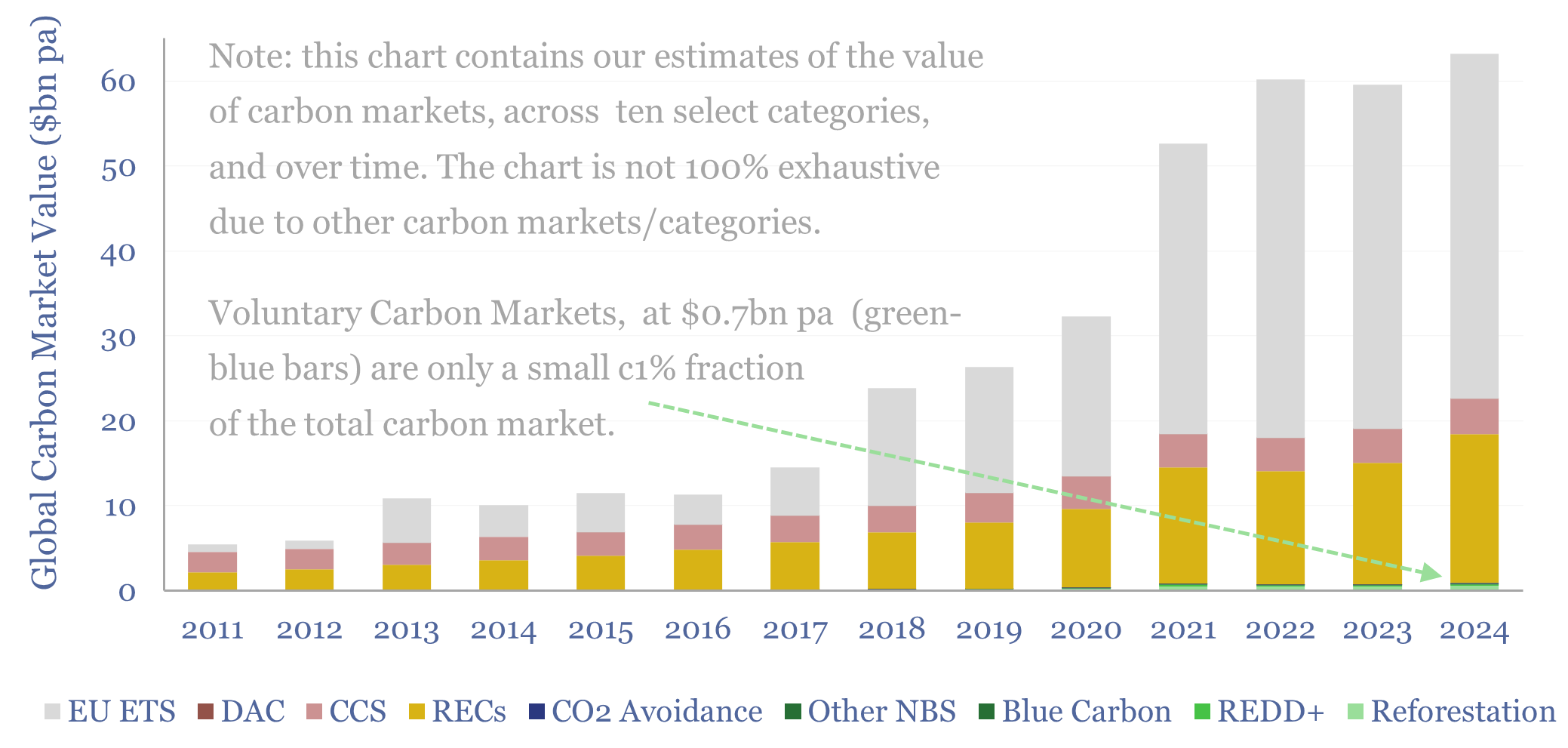
Carbon markets: by category over time?
This data-file quantifies global carbon markets by category over time, including the EU ETS as an example of a compliance market, RECs, CCS and VERRA-certified “carbon credits”, across categories such as REDD, reforestation and other “carbon offsets”. We also draw analogies with charitable giving and forecast carbon markets out to 2050.
-
Commodity prices: metals, materials and chemicals?
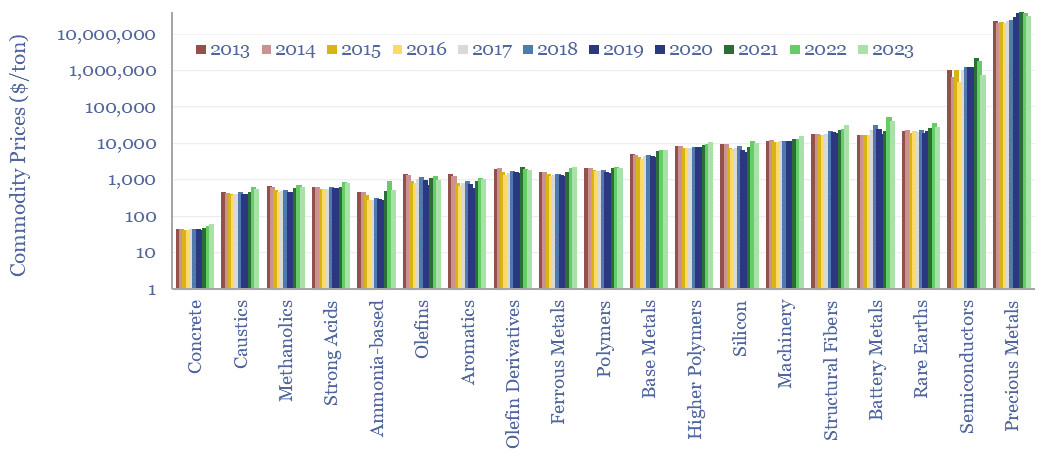
Annual commodity prices are tabulated in this database for 70 materials commodities; covering steel prices, other metal prices, chemicals prices, polymer prices, all with data going back to 2012. 2022 was a record year for commodities. The average material commodity traded 25% above its 10-year average and 60% of all material commodities made ten-year highs.
-
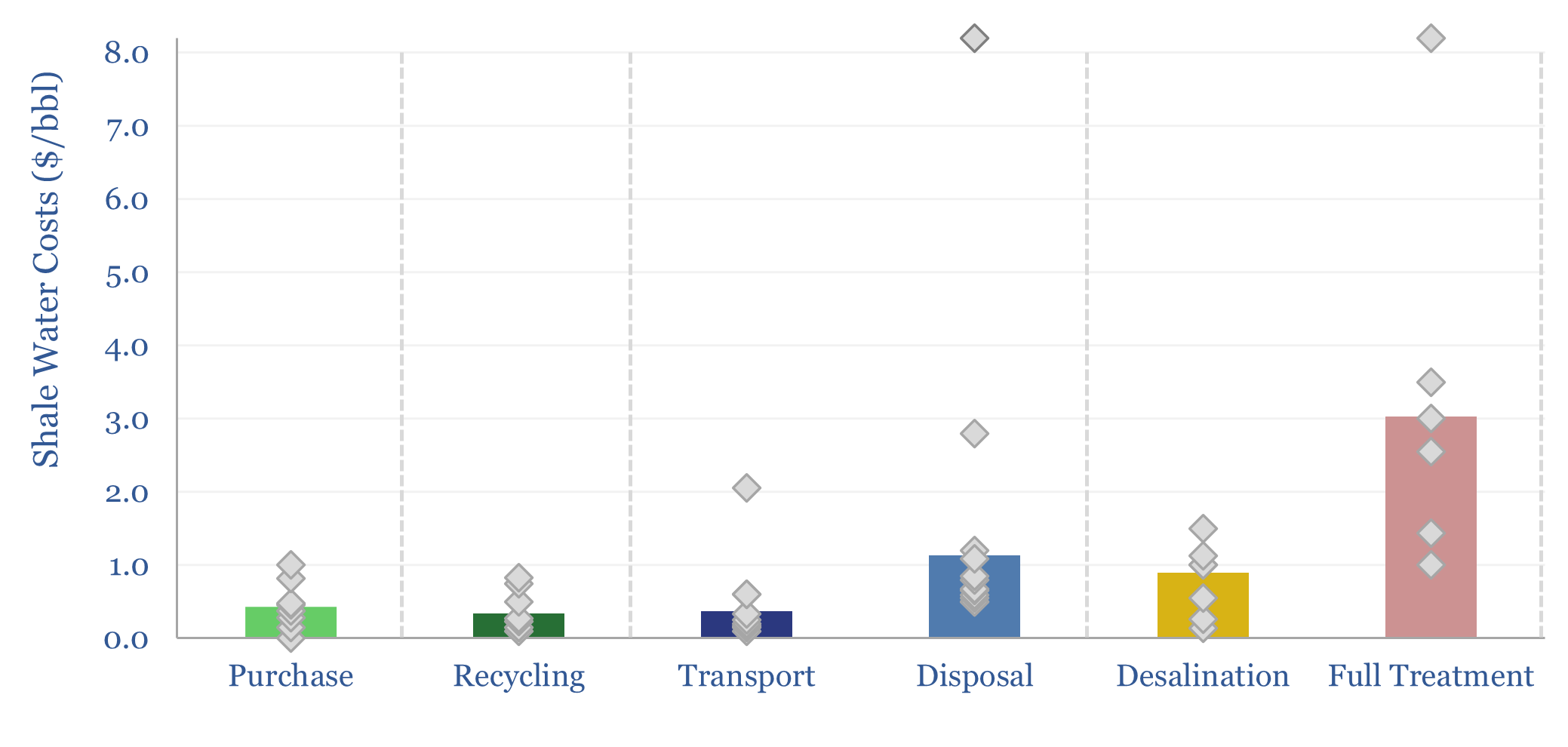
Shale water costs: transport, treatment and disposal?
Shale water costs might average $0.3/bbl for filtering and recycling, $0.4/bbl to procure new water, $1/bbl for disposal and $3/bbl for full treatment back to agricultural/cooling-quality water. There is variability in water properties and throughout shale basins. This data-file aggregates disclosures into shale water costs.
-
Load profiles in power grids?
Load profiles depict how the power running through a particular cross-section of the grid varies over time, ranging from individual homes, through giant GVA-scale transmission lines. Load profile data are unfortunately not widely available, however, we have aggregated a dozen case studies from technical papers, in this data-file, to help decision-makers with grid-modeling.
-
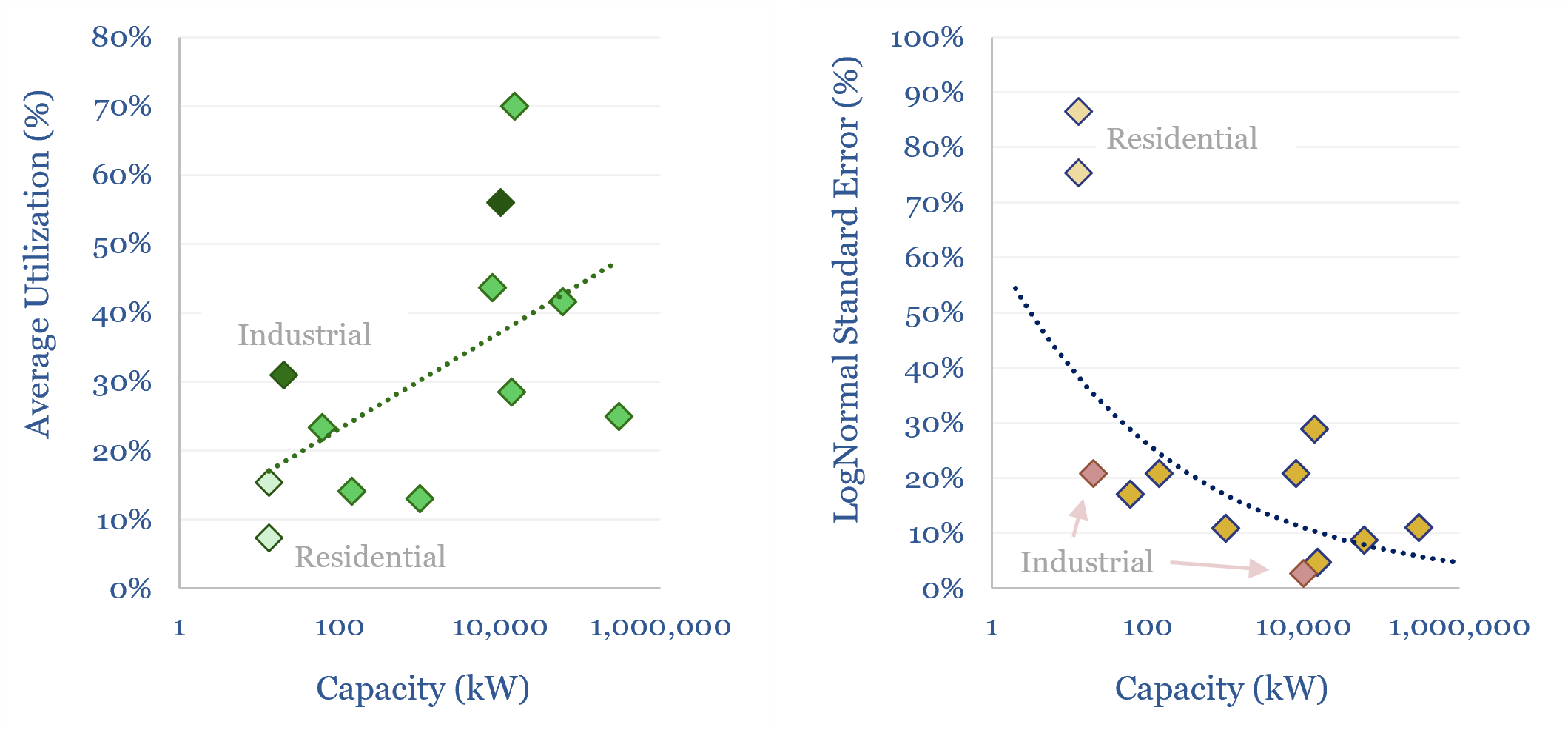
Wind turbine capacity factors: by country, by facility?
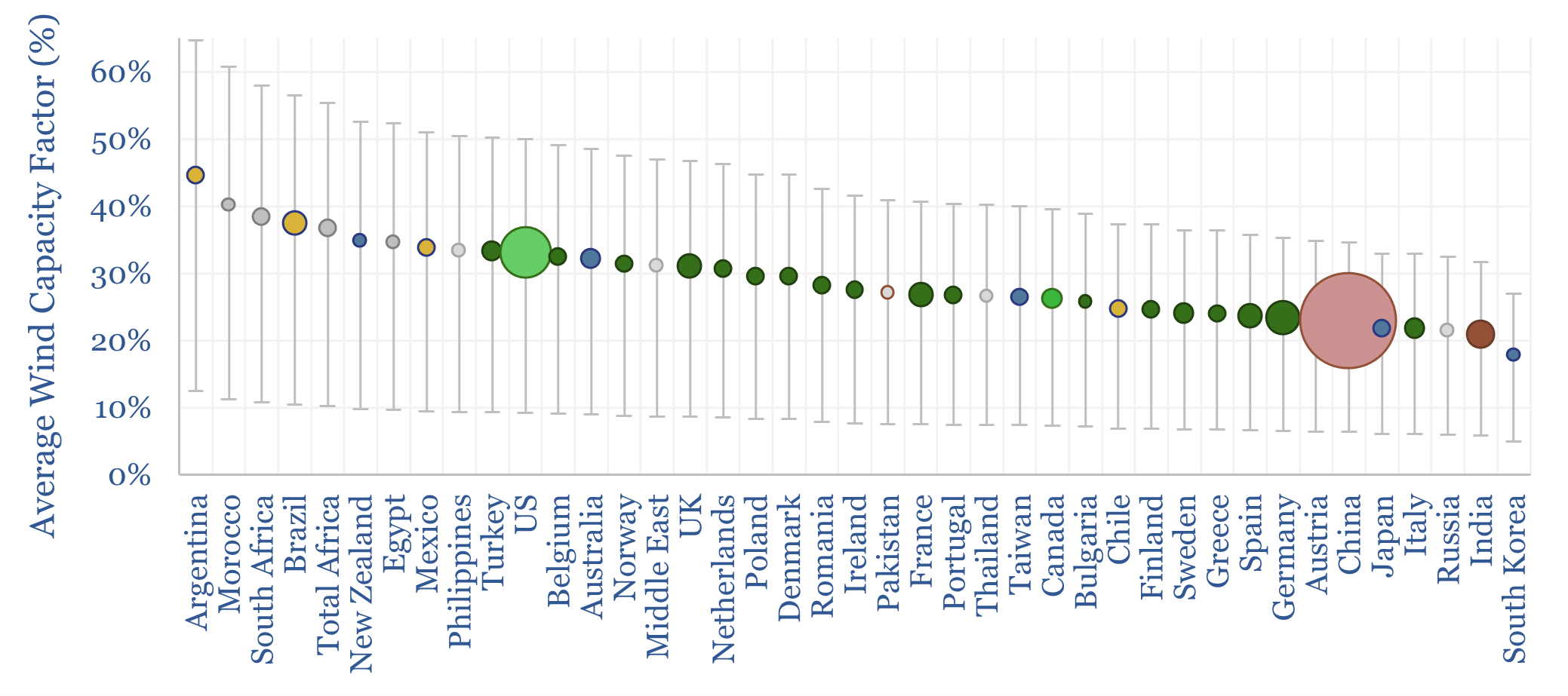
Wind turbine capacity factors average 26% globally. But they vary from c20% in non-windy countries to 45% in the windiest countries. And they also vary within countries, with a normal distribution and a standard deviation of 7-12%. This data-file maps capacity factors of wind power generation.
-
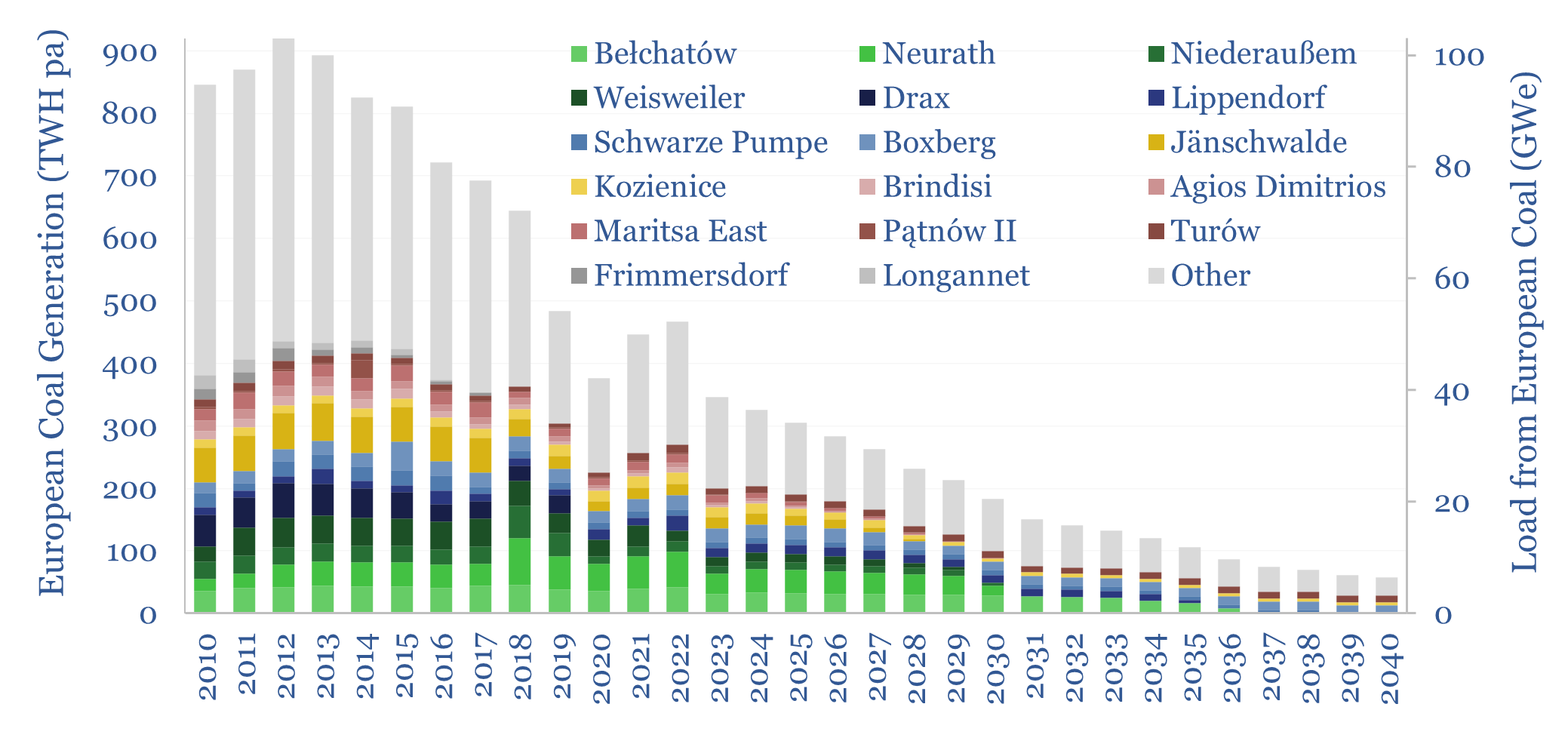
European coal generation by facility and coal plant closures?
Europe generated 350TWH of electricity from coal in 2023, having halved over the prior decade, and potentially declining to zero around 2040. We have recently been wondering whether this phase-back of coal is compatible with geopolitical priorities or the need to keep pace with the rise of AI. Hence this data-file tracks European coal generation…
-
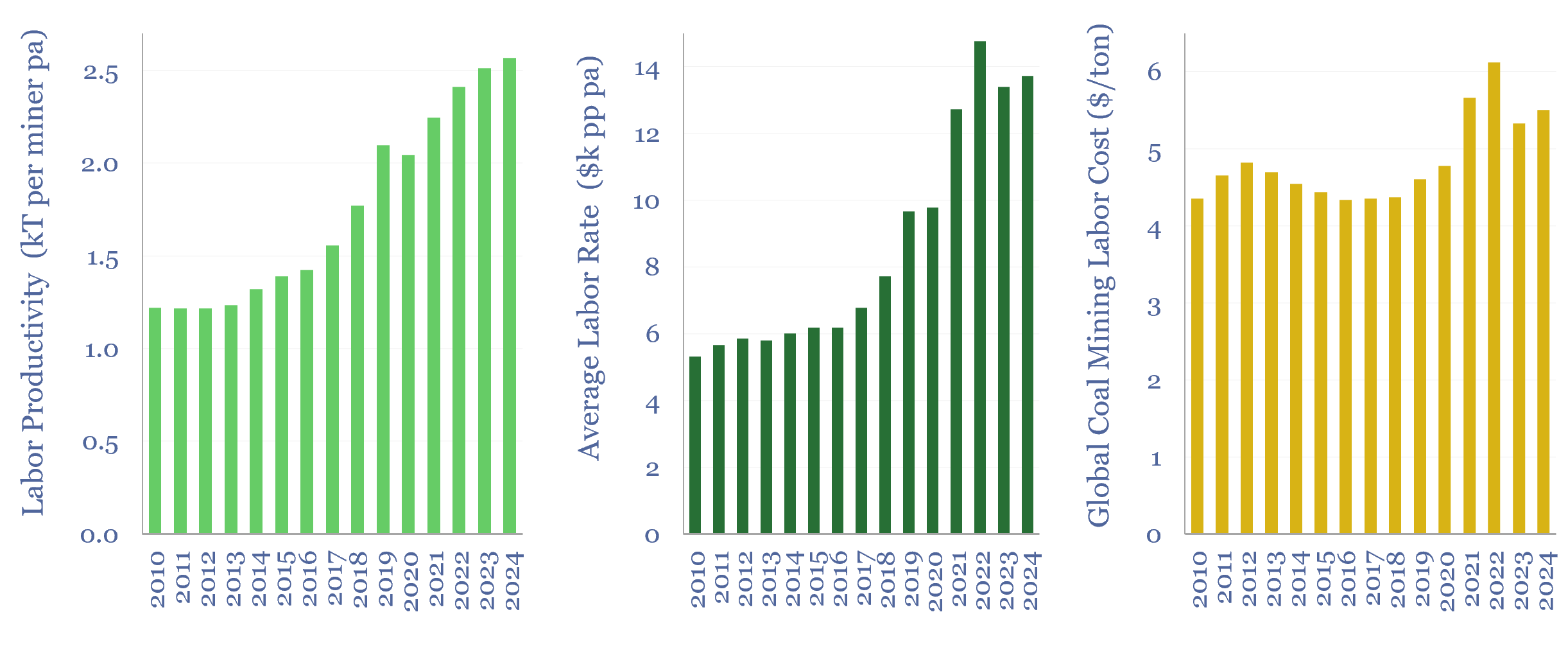
Labor costs of coal production: labor productivity and salaries?
This data-file estimates the labor costs of coal production, as a function of labor productivities and salaries, by region and over time. As a global average, across the 3M global coal mine employees captured in the data-file, labor productivity runs at 2,500 tons of coal per employee per year, average salary is $14k pp pa,…
-
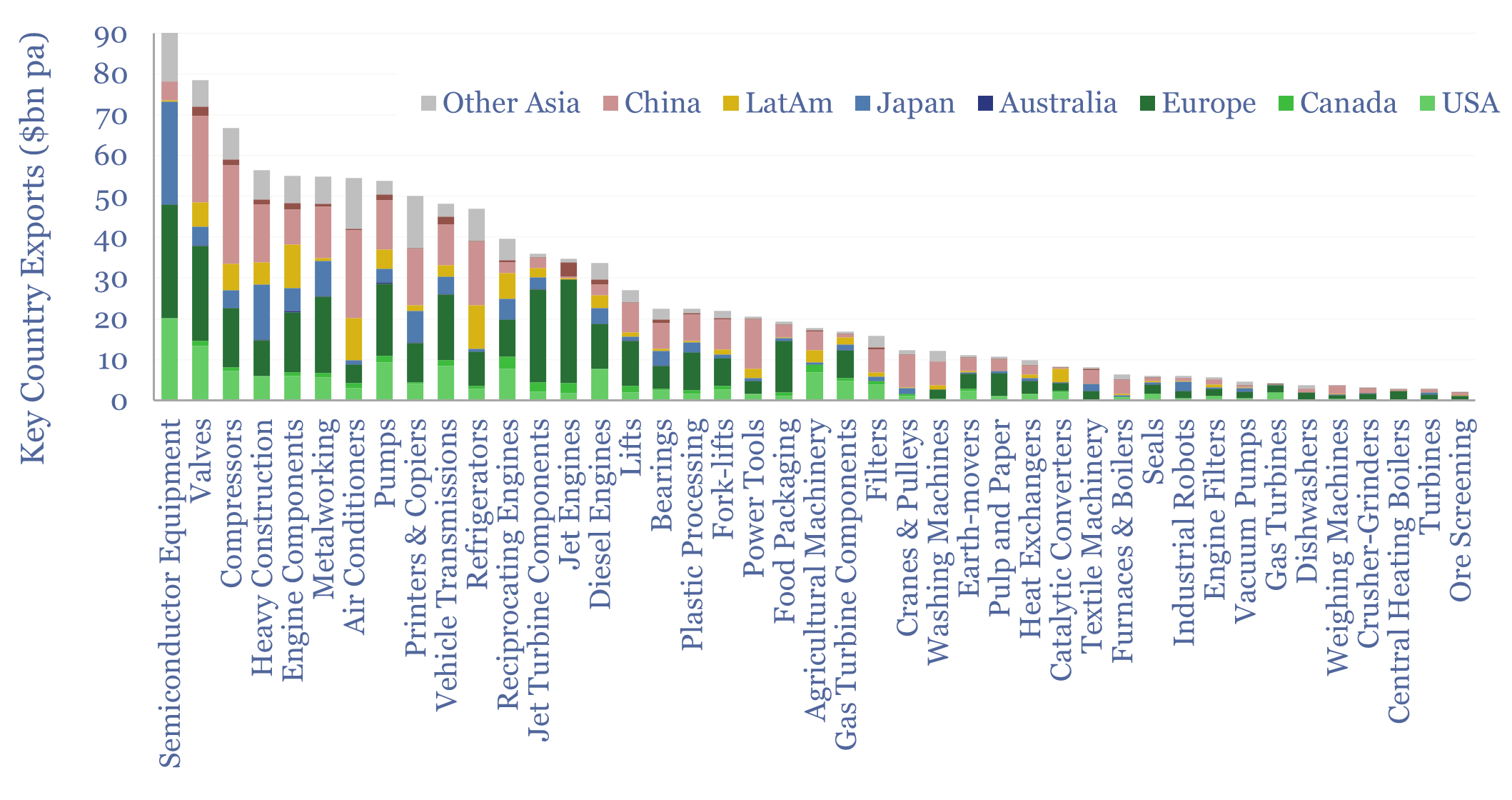
Capital goods market sizes: by category, by country?
This data-file tabulates globally traded capital goods market sizes, based on the values of products exported from different countries-regions. Specifically, commodity Code 84 represents machinery and mechanical appliances, worth $2.5trn pa in 2023. About half of that represents classic capital goods categories, as decomposed in the chart above. Our top five conclusions follow below.
-
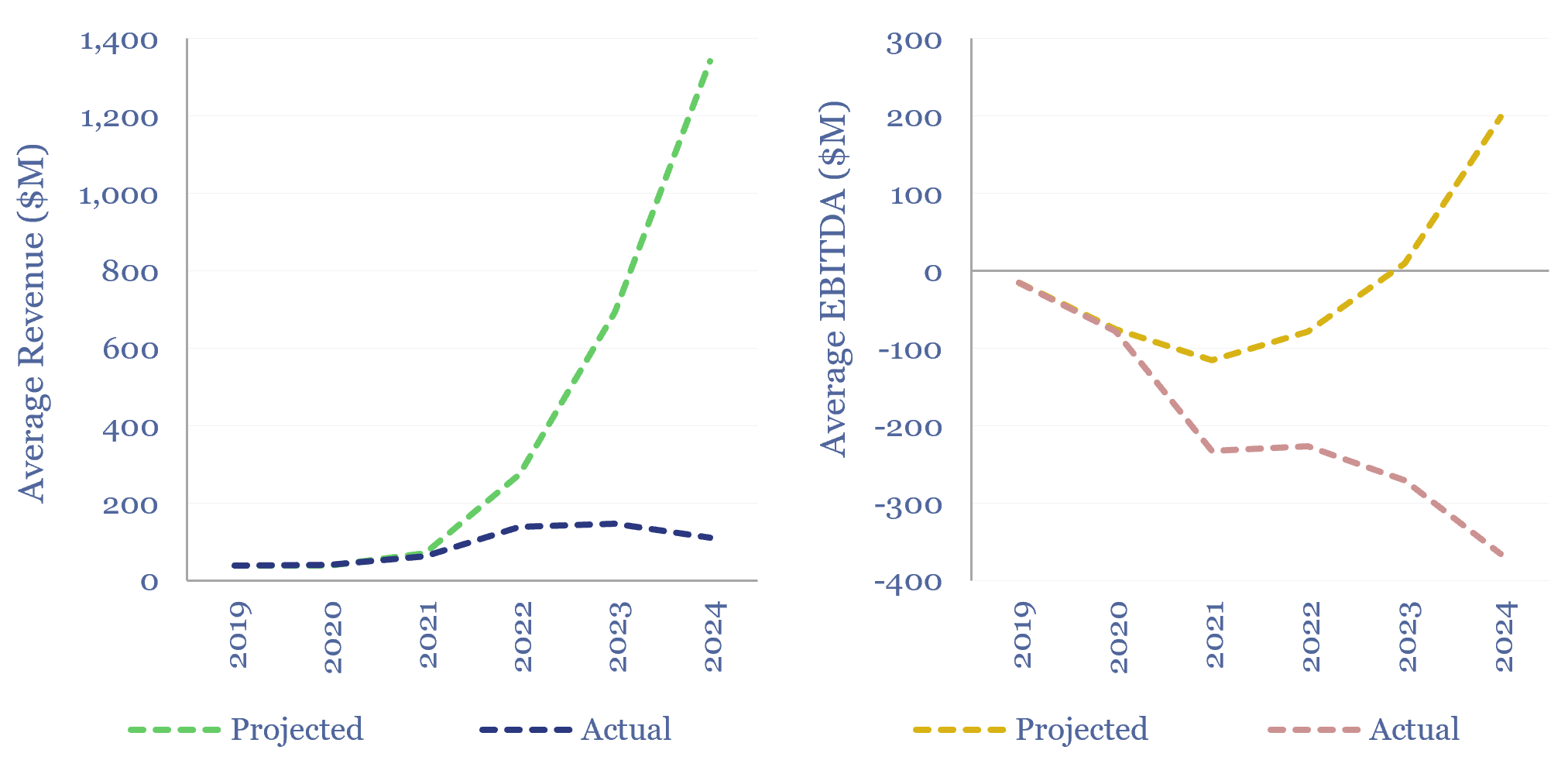
Early-stage companies: growth versus projections?
Early-stage companies’ growth versus projections is assessed in this data-file, tabulating the performance of 20 new energies SPACs from 2020-21. The average of these companies was projecting that its revenues would explode to $1.3bn by 2024, but in reality, revenue only trebled to $110M. On average, 2024 EBITDA also missed aspirations from 2020-21 by $350M.…
-
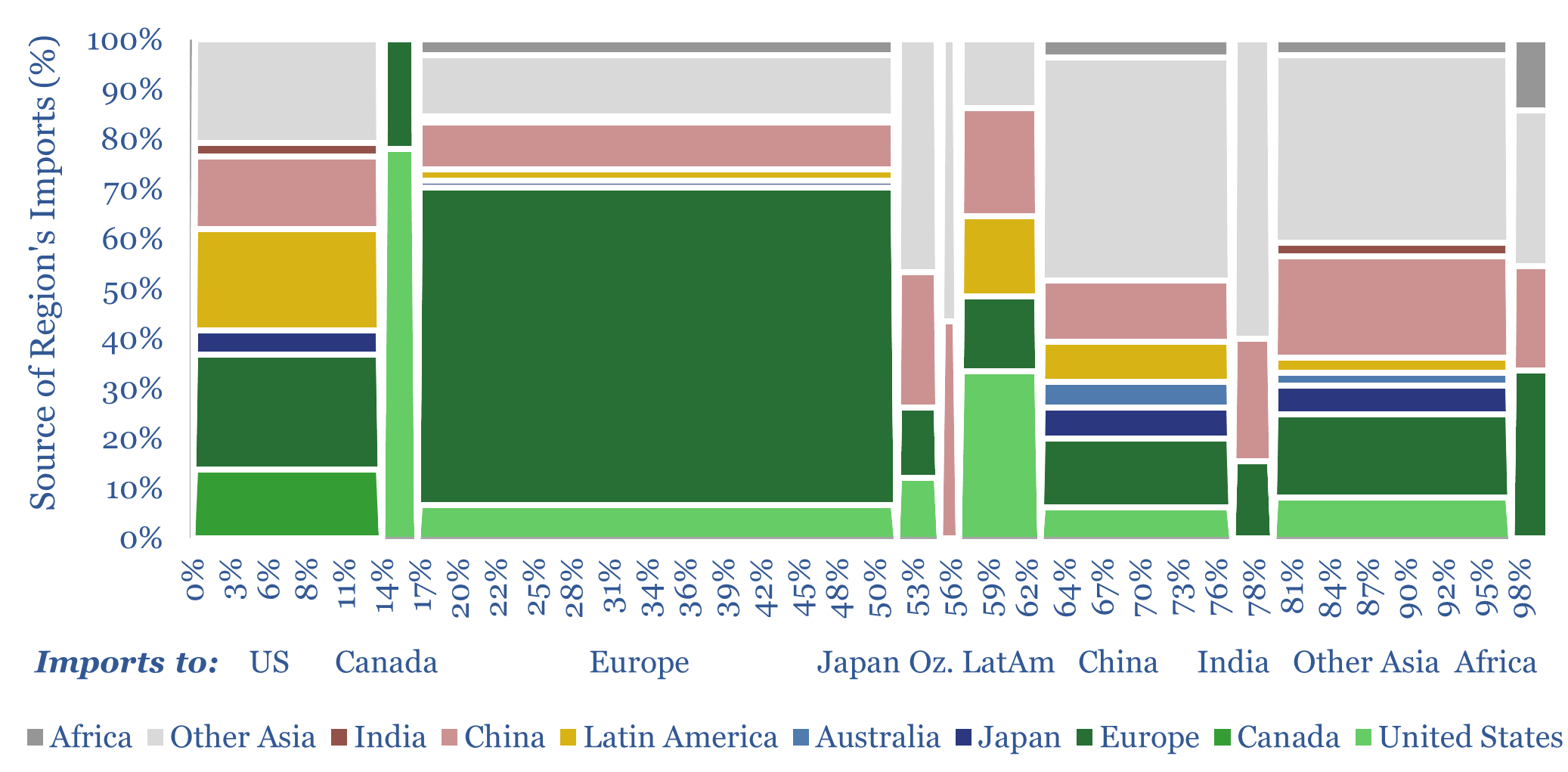
Global trade: imports and exports, by product, by region?
Global trade is set to hit a new peak of $33trn in 2024 (30% of global GDP), of which 70-80% is for goods and 20-30% is for services. This data-file disaggregates global trade by product by region, across c20 categories of energy, materials and capital goods, which we follow in our research, and which are…
Content by Category
- Batteries (85)
- Biofuels (42)
- Carbon Intensity (49)
- CCS (63)
- CO2 Removals (9)
- Coal (38)
- Company Diligence (88)
- Data Models (808)
- Decarbonization (158)
- Demand (106)
- Digital (52)
- Downstream (44)
- Economic Model (196)
- Energy Efficiency (75)
- Hydrogen (63)
- Industry Data (270)
- LNG (48)
- Materials (79)
- Metals (70)
- Midstream (43)
- Natural Gas (146)
- Nature (76)
- Nuclear (22)
- Oil (162)
- Patents (38)
- Plastics (44)
- Power Grids (119)
- Renewables (149)
- Screen (110)
- Semiconductors (30)
- Shale (51)
- Solar (67)
- Supply-Demand (45)
- Vehicles (90)
- Wind (43)
- Written Research (342)