This data-file is an overview of wind power physics. Specifically, how is the power of a wind turbine calculated, in MW, as a function of wind speed, blade length, blade number, rotational speed (in RPM) and other efficiency factors (lambda). A large, modern offshore wind turbine will have 100m blades and surpass 10MW power outputs.
Wind turbines generate power as an incoming mass of air transfers its energy into the turbine as it slows down. The formula for kinetic energy is 0.5 x mass x velocity^2. Mass must be conserved upstream and downstream of the wind turbine. Hence via some simple maths, the energy that can be harvested by the turbine equates to 0.5 x mass of air x (incoming velocity immediately upstream of the turbine ^ 2 – outgoing velocity immediately downstream of the turbine ^ 2).
What is the mass of air? It is useful to note that the mass of air passing the turbine can be broken down further as density of air x volume of air flowing past the turbine per second. In turn, the volume of air flowing past the turbine per second can be broken down as the cross sectional area of the turbine (pi x blade length ^ 2) multiplied by the velocity of the air in meters per second. Time to do some simple multiplication…
What is the best formula for a wind turbine’s power output? The best overall formula for the power derived from a wind turbine (in Watts) is P = 0.5 Cp ρ π R2 V3, where Cp is the coefficient of performance (efficiency factor, in percent), ρ is air density (in kg/m3), R is the blade length (in meters) and V is the wind speed (in meters per second).
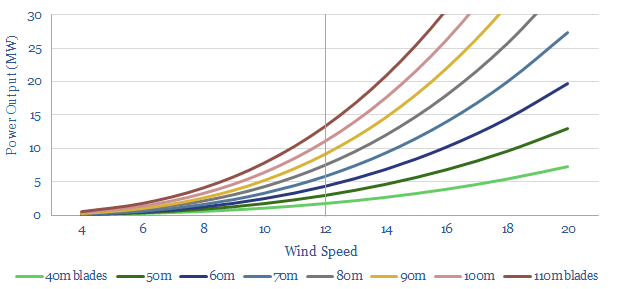
Location matters most. The formula above shows that the power output of a wind turbine is a cube function of incoming wind velocity. Thus if you can access a 2x windier location (e.g., 12 m/s versus 6 m/s), this does not simply double the available power output. It octuples it (2^3=8). This explains the industry’s push towards offshore wind, where wind speeds are higher. And the quest for ever-taller towers, to access faster wind speeds at greater heights. But unfortunately, it also explains why non-windy regions, including regions in the wind shadow of large mountain ranges, will always have low wind potential (US examples here).
The trend towards large blades. Our formula above also showed that the potential power generation of a wind turbine is a square function of its blade length. Doubling the blade length from 50 meters to 100 meters might thus increase the potential power output by a factor of four (2^2=4), from around 3MW to 12MW. This explains the industry’s push to ever larger blades using incredible materials such as carbon fiber, glass fiber and specialist resins.
What is Betz’s limit on a wind turbine’s efficiency? One of the terms in our power formula above was Cp, which is the ‘coefficient of performance’, or the percent of maximum possible energy that can be harvested from the air hitting the wind turbine. It is an immutable law of physics that the absolute maximum theoretical efficiency of any turbine is 59.3% (16/27). This limit is reached when the wind slows down by precisely two-thirds as it passes the turbine. The maths are derived in the data-file. But the key idea is that if a wind turbine was going to harvest ALL of the energy in the incoming air flow, and slow the speed of outgoing air flow to zero, then by the law of conservation of mass, that outgoing air flow would need to fan out across an infinitely wide cross sectional area, which is clearly impossible. At maximum efficiency, the column of air fans out over a 3x larger area.
What are the real world limits on a wind turbine’s efficiency? If you want a good, simple estimate for the coefficient of performance, you can assume that a real world wind turbine might achieve a Cp of 35-45%. In other words, it will capture 35-45% of the total available incoming wind energy. If this energy is going to be harnessed for useful work, then there may also be small additional losses for important power electronics, transformers and power transmission.
What determines the efficiency of a wind turbine in the real world? The Betz limit applies to an idealized wind turbine, which has an infinite number of rotor blades with no drag. Real-world turbines have a finite number of blades. Usually three. And thus the coefficient of performance will depend on how fast these blades spin. If the blades do not spin fast enough, then air will simply flow between the gaps in the blades and its energy will not be captured. If the blades spin too fast, then they will “collide with” the turbulence trailing in the wake of the preceding blades, which is not fully exposed to the incoming wind, and thus they will also capture a lower share of the incoming wind’s energy.
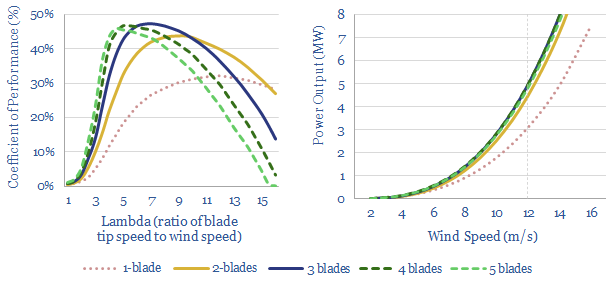
What is the optimal speed for a wind turbine to rotate? Tip speed ratio (lambda) denotes the ratio of the blade tip’s speed divided by the wind speed. Usually the optimal lambda value is around 7 for a three-blade wind turbine, equating to 10-20 rpm when incoming wind speeds are 6-12 meters per second. For the full maths, the optimal wind speed ratio is calculated in the data-file. But it is interesting to note that the optimal rotational speed of a wind turbine rises with wind speed, falls with the length of the blades, and falls with number of blades.
Why does a wind turbine have three blades? The short answer is “maths”. The slightly longer answer is that a three-blade turbine gives the best trade-off between high efficiency factors within common lambda values of 4-10 (chart above left) and low costs. The full answer adds further considerations. Three blade turbines also balance high stability, low noise, pleasing aesthetics and not needing to over-invest in an excessive number of turbine blades.
When is it logical for a wind turbine to have more blades? A turbine with more blades will generate more torque. But it will also turn more slowly, as each blade creates additional air resistance and turbulence. Additional blades also add cost. Hence it can make sense to have more blades (5-blades to 13-blades) for small-scale wind turbines in residential/light commercial settings. These are exposed to slower incoming wind speeds so the extra torque helps. It can increase output by 60% compared with a three blade turbine. Slower rotational speeds mean lower noise. And it does not hurt the economics too much, as these small blades are a lower portion of total wind turbine cost compared to the 100-meter monster blades installed in very large offshore wind turbines.
Could large wind turbines shift to using two blades? Another intriguing observation from the physics is the possibility of two-blade turbines, as an adaptation strategy that is open to the offshore wind industry, if material costs inflate too much. The physics dictate that a two blade turbine will need to rotate around 30% faster than a three-blade turbine, and despite this, efficiency will likely still be around 3-10% lower. However, the largest blades in the industry cost $0.5-1.0M apiece. By taking out an entire blade, the turbine’s total costs could be 7-20% lower (again, as derived from our wind turbine cost models).
Stability issues for even-numbered blades? On the other hand, maintenance costs of wind turbines are likely to be higher for turbines with even numbers of blades, because of their symmetry. One example of this elevated stress level occurs when two symmetrical blades are oriented vertically: The bottom blade is in the ‘wind shadow’ of the tower at the exact moment when the top blade is at its apogee, and thus experiencing the greatest lever arc force. Another example of elevated stress occurs when two symmetrical blades are both oriented horizontally: this doubles the strain running through the center of the turbine. These forces can cause the blades to vibrate, resonate, even fail. And thus the need to reinforce even-numbered turbines may offset some of the cost savings noted above. Seeking to overcome some of these challenges, companies such as Seawind Ocean Technologies, CoFlow Jet Wind Turbines and Chinese giant Ming Yang Wind Power have all been exploring two-blade concepts.
Other complexities. In the real world, theoretical mechanics are a good guide, but it becomes necessary to switch to empirical models. A wind turbine blade has a complex aerodynamic profile: wider at the base, thinner at the tip, shaped like an airfoil to generate lift that counteracts drag, and with a twisted pitch angled 10-15 degrees more at the base. Rather than passing through the turbine, the wind will also eddy and rotate. And in a large wind farm, the aerodynamic impact of one wind turbine will impact others nearby. Hence the Cp values in this model are tabulated from empirical studies, not calculated.
How is the power output of a wind turbine calculated? The full data-file breaks down the physics of wind power turbines, to approximate wind power generation in MW, in a simple c20-line model, for anyone that is particularly interested in the modelling.