Electromagnetic radiation is a form of energy, exemplified by light, infrared, ultraviolet, microwaves and radio waves. What is the energy content of light? How much of it can be captured in a solar module? And what implications? We answer these questions by modelling the Planck Equation and Shockley-Queisser limit from first principles.
Electromagnetic radiation is the synchronized, energy-carrying oscillation of electric and magnetic fields, which moves through a vacuum at the speed of light, which is 300,000 km per second.
Most familiar is visible light, with wavelengths of 400 nm (violet) to 700 nm (red), equating to frequencies of 430 (red) to 750 THz (violet).
At the center of the solar system, our sun happens to emit c40% of its energy in the visible spectrum, 50% as infra-red and c10% as ultraviolet, and very little else (e.g., X-rays, gamma rays at high frequency; microwaves and radio waves at high wavelength). But this is not a coincidence…
Planck’s Law: Spectral radiance as a function of temperature?
Planck’s Law quantifies the electromagnetic energy that will be radiated from a body of heat, across different electromagnetic frequencies, according to its temperature, the speed of light, Boltzmann’s constant (in J/ºK) and Planck’s constant (in J/Hz).
In the chart below, we have run Planck’s equation for radiating bodies at different temperatures from 3,000-8,000ºK, including the sun, whose surface is 5,772ºK. Then we have translated the units into kW per m2 of surface area and per nm of wavelength.
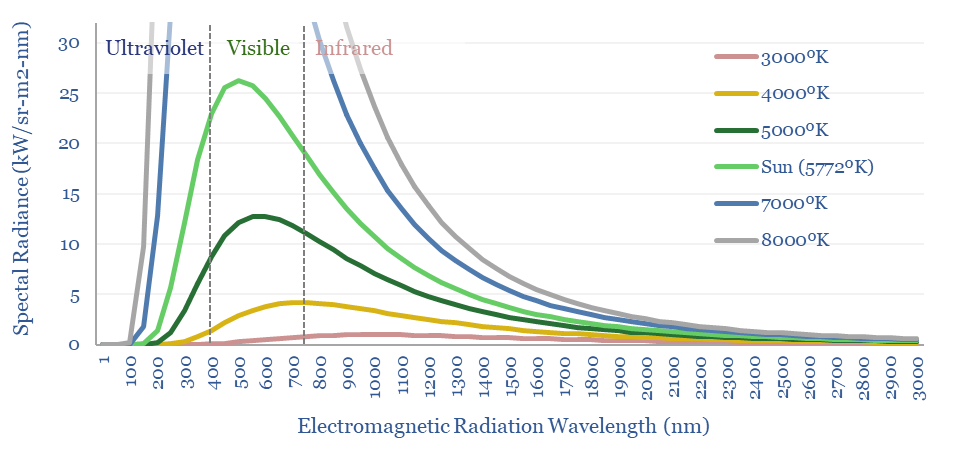
Hence by integration, the ‘area under the curve’ shows the total quantity of electromagnetic radiation per m2. If the surface of the sun were just 10% hotter, then it would emit c50% more electromagnetic radiation and 55% more visible light!
Charts like this also explain why the filament of an incandescent light bulb, super-heated to 2000-3000ºC is only going to release 2-10% of its energy as light. Most of the electromagnetic radiation is in the infra-red range here. And this is the reason for preferring LED lighting as a more efficient alternative. LEDs can reach 60-90% efficiency.
Planck’s Law and Solar Efficiency?
Planck’s Law also matters for the maximum efficiency of a solar module, and can be used to derive the famous Shockley-Queisser limit from first principles, which says that a single-junction solar cell can never be more than c30-33% efficient at harnessing the energy in sunlight.
Semiconductor material has a bandgap, which is the amount of energy needed to promote a single electron from its valence band into its conduction band: a higher energy state, from which electricity can be drawn out of a solar cell. For silicon, the bandgap is 1.1 eV.
What provides the energy is photons in light. The energy per photon can be calculated according to its wavelength. This involves multiplying Planck’s constant by the Speed of Light, dividing by the wavelength, and then converting from Joules to electronVolts. For a radiating body at 5,772ºK, the statistical distribution of photons and their energies is below.
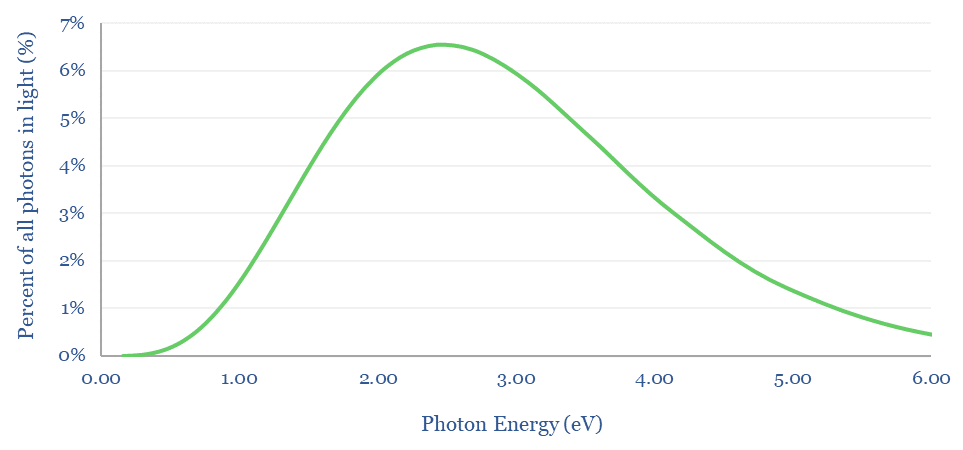
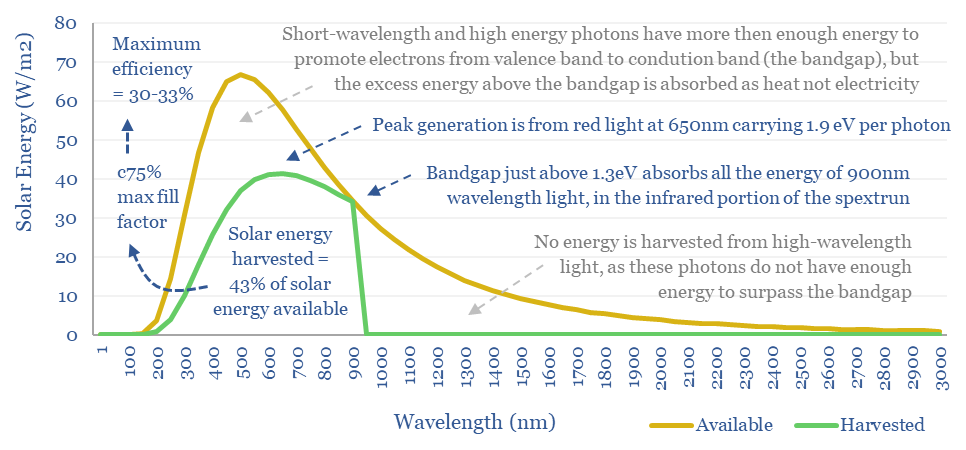
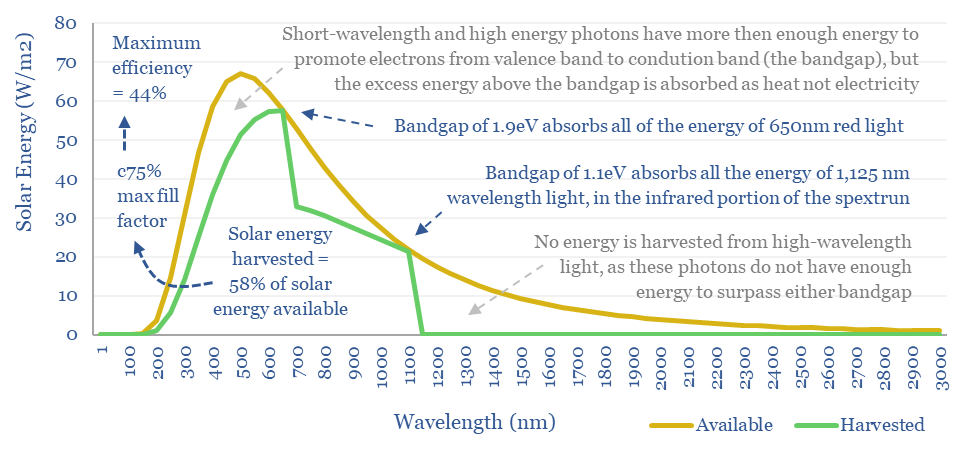
So what bandgap semiconductor is best? If the bandgap is too high (e.g., 4eV), then most of the photons in light will not contain sufficient energy to promote valence band electrons into the conduction band, so they cannot be harnessed. Conversely, if the bandgap is too low (e.g., 0.5eV), then most of the energy in photons will be absorbed as heat not electricity (e.g., a photon with 2.0 eV would transfer 0.5eV into electron promotion, but the remaining 1.5 eV simply heats up the cell).
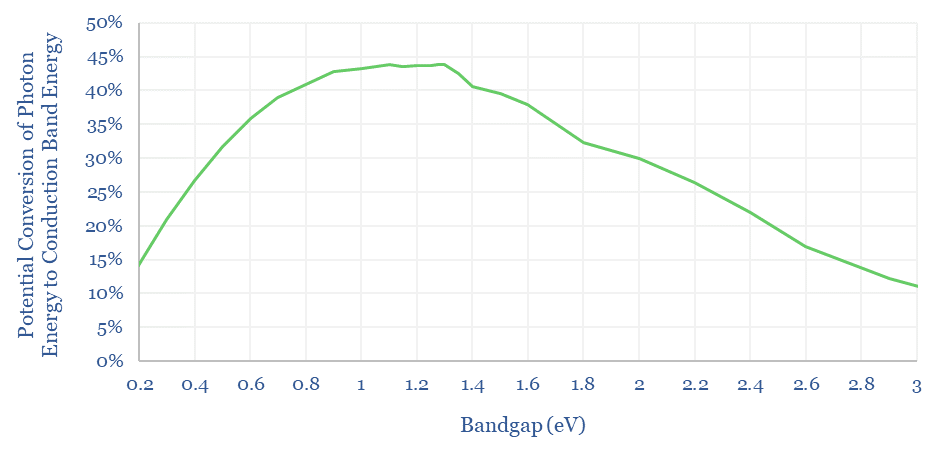
The mathematical answer is that a bandgap just above 1.3 eV maximizes the percent of incoming sunlight energy that can be transferred into promoting electrons within a solar cell from their valence bands to their conduction bands, at 43-44% (chart below).
If we run a sensitivity analysis on the bandgap, the next chart below shows that our 43-44% conversion limit holds for any semiconductors with a bandgap of 1.1-1.35eV, more of a plateau than a sharp peak.
The Shockley-Queisser limit is usually quoted at 30-34%, which is lower than the number above. In addition to the losses due to incomplete capture of photon energy, the maximum fill factor of a solar cell (balancing load, voltage and current) is around 77%, so only 77% x 44% = 34% of the incoming light energy could actually be harnessed as electrical energy. Moreover, in their original 1961 paper, Shockley and Queisser assumed an 87% efficiency limit for impedance matching relative to the 77%, which is why the number they originally quoted was around 30%.
Another issue is that the solar energy arriving at a given point on Earth has been depleted in certain wavelengths, as they are absorbed by the atmosphere. 1,362W/m2 of sunlight reaches the top of the Earth’s atmosphere. While on a clear day, only around 1,000W/m2 makes it to sea level at the equator. We know the atmosphere absorbs specific infrared wavelengths as heat, because this is the entire reason for worrying about the radiative forcing of CO2 or radiative forcing of methane.
Hence for an ultra-precise calculation of maximum solar efficiency, we should not take the Planck curve, but read-out the solar spectrum reaching a particular point on Earth, which will itself vary with weather!!
Multi-junction solar is inevitable?
The biggest limitation on the efficiency of single-junction solar cells is that they only contain a single junction. This follows from the discussion above. But what if we combine two semiconductors, with two bandgaps into a ‘tandem cell’. The top layer has a bandgap of 1.9eV (e.g. perovskite) and the second has a bandgap of 1.1eV (e.g., silicon). The same analysis now shows how the maximum efficiency can reach 44%.
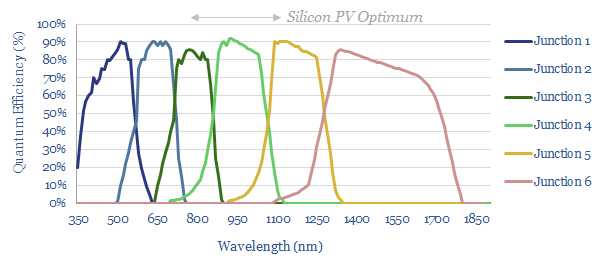
Cells with multiple semiconductors are already being commercialized. For example, we wrote last year about heterojunction solar (HJT) and this year about the push towards perovskite tandems in solar patents from LONGi. It feels like the ultimate goal will be multi-junction cells that capture along the entire solar spectrum (chart below). It will simply take improvements in semiconductor manufacturing.
Power Beaming and Other
Elsewhere in the electromagnetic spectrum, this data-file also contains workings into the energy efficiency of microwave energy, transmitting it through space and converting it back to useful electricity via rectennas.
All of the numbers and calculations go back to first principles, in case you are looking to model the Planck Equation, Shockley-Queisser limit, multi-junction solar efficiency, lighting efficiency, or other calculations of electromagnetic radiation energy.
