How does atmospheric CO2 increase global temperature? The purpose of this article is to outline the best formulae we have found linking global temperature to the concentration of CO2 in the atmosphere. In other words, our goal is a simple equation, explaining how CO2 causes warming, which we can use in our models. In turn, this is why our ‘roadmap to net zero’ aims to reach net zero by 2050, stabilize atmospheric CO2 at 450ppm, and we believe this scenario is compatible with 2ºC of warming.
Disclaimer: can a simple equation explain global warming?
Please allow us to start this short note with a disclaimer. We understand that writing anything at all about climate science is apt to incur the unbridled wrath of substantively everyone. We also understand that the world’s climate is complex, and cannot be perfectly captured by simple formulas, any more than ‘world history’ can be.
Nevertheless, the over-arching goal of all of our research is that we are trying to model the best roadmap to decarbonize the global energy system (note below), and the best resultant opportunities in the energy transition.
Hence we think it is useful to have an approximate formula, even if it is only “about 80% right”, rather than a conceptual black hole. So that is the purpose of today’s short note.
(1) Thermal theory: inflows and outflows?
The Earth’s temperature will be in balance and remain constant if energy inflows match energy outflows. Energy inflows come from the sun, and are approximated by the ‘solar constant’, at 1,361 W/m2. Energy outflows are radiated back into space, and are approximated by the Stefan-Boltzmann law.
One of the terms in the Stefan-Boltzmann equation is Temperature^4. That is temperature raised to the power of four. In other words, if for some reason, the Earth is not quite radiating/reflecting 1,361 W/m2-equivalent back into space, then its average temperature needs to become a little bit warmer, until it is once again radiating 1,361 W/m2-equivalent back into space. Let’s unpack this bit further…
Physics dictates that any physical body with a temperature above absolute zero will radiate energy from its surface, usually small amounts of energy. The wavelength depends on the body’s chemical properties, and more importantly, its temperature, i.e., its thermal energy.
Energy is the inverse of wavelength. Some electromagnetic radiation has a wavelength of 380-700 nm, in which case we call this radiation ‘visible light’. Some has lower energy, and thus higher wavelength. For example, radiation with a wavelength of 700-1,000 nm is often referred to as ‘infra-red’.
So in conclusion, energy is constantly being radiated back “upwards” towards outer space by the Earth’s surface, i.e., its land and its seas. These wavelengths are generally in the infra-red range. They span from 600 – 20,000 nm. But how much of that energy actually escapes into space?
(2) Greenhouse Gases: CO2, CH4, N2O, et al.
CO2 is a greenhouse gas. This means that as thermal energy is radiated upwards from the Earth’s surface — land and sea — it can excite the electrons in CO2 molecules, into a higher energy state, for a few nano-seconds. These electrons quickly relax back into a lower-energy state. As they do this, they re-radiate energy.
In other words, CO2 molecules absorb energy that is “meant to be” radiating upwards from the Earth’s surface back into space, and instead they scatter it in various other directions, so some of it will be re-absorbed (e.g., back in the world’s oceans).
In passing, this is why some scientists object to CO2 being described as ‘a blanket’. It is not trapping heat. Or storing any heat itself. It is simply re-radiating and re-scattering heat that would otherwise be travelling in a more direct path back into space.
This effect of CO2, and other greenhouse gases, can be described as ‘radiative forcing’ and measured in W/m2. In 2021, with 416ppm of CO2 in the atmosphere, the radiative forcing of atmospheric CO2 is said to be 2.1 W/m2 higher than it was in 1750, back when there was 280 ppm of CO2 in the atmosphere.
So what equations relate atmospheric CO2 concentrations into radiative forcing effects and ultimately into temperatures?
(3) Absorbing equations: how does CO2 impact temperature?
Let us start with an analogy. You are reading a complicated text (maybe this one). On the first reading, you absorb and retain about 50% of the content. One the second reading, you absorb and retain another 25% of the content. On the third reading, you absorb another 13% of the content. And so on. By the tenth reading, you have absorbed 99.9% of the content. But the general idea is that the more you have absorbed on previous readings, the less is left to be absorbed on future readings.
The absorption profile of CO2 is similar. One way to think about this is that even a very small amount of a particular greenhouse gas is going to start absorbing and re-radiating energy at its particular absorption wavelengths. This dilutes the amount of energy with this particular wavelength that remains. This means that there will be less energy with this particular wavelength left to absorb by adding more of molecules of this greenhouse gas into the atmosphere. By definition, the additional gas is ‘trying to’ absorb radiation at a wavelength that is already depleted.
Hence, without any CO2 in the atmosphere, the Earth would be about 6C cooler. The first 20ppm of CO2 explains perhaps 2ºC of all the warming exerted by CO2. The next 20ppm explains 0.8ºC. The next 20ppm explains around 0.6ºC. And so on. There are diminishing returns to adding more and more CO2.
Systems like this are described with logarithmic equations. Thus in the past, the IPCC has suggested various log equations that can relate radiative forcing to atmospheric CO2. The most famous and widely cited formula is below:
Increase in Radiative Forcing (W/m2) = 5.35 x ln (C/C0) … where C is the present concentration of atmospheric CO2 in ppm; and C0 was the concentration of atmospheric CO2 in 1750, which was 280 ppm.
The scalar value of 5.35, in turn, is derived from “radiative transfer calculations with three-dimensional climatological meteorological input data” (source: Myhre, G., E. J. Highwood, K. P. Shine, and F. Stordal, (1998). New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett., 25, 2715–2718). Note these formulae are quite long-standing and go back to 1998-2001.
Thus in the chart below, we have averaged three log formulas, suggested in the past by the IPCC, to calculate radiative forcing from atmospheric CO2. Next, to translate from radiative forcing into temperature we have used a “gamma factor” of 0.5ºC per W/m2 of radiative forcing, which is also a number suggested in the past by the IPCC.
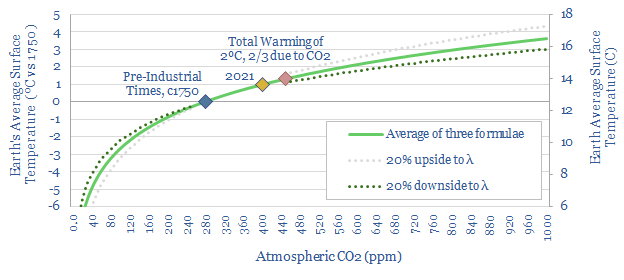
(4) Temperature versus CO2: mathematical implications?
Let us interpret this chart above from left to right. This is intended to be an objective, mathematical exercise, assessing the implications of simple climate formulae proposed long ago by the IPCC.
(a) Much of the greenhouse effect has “already happened“, due to the log relationship in the chart. The chart implies that the total greenhouse effect occurring today from atmospheric CO2 is around 7-8ºC, of which c6-7ºC was already occurring back in 1750.
(b) Raising atmospheric CO2 to 415ppm should have increased global temperatures by around 1ºC since pre-industrial times, just due to CO2, and holding everything else equal, again just taking the IPCC’s formulae at face value.
(c) Raising atmospheric CO2 by another 35ppm to 450ppm would, according to the simple formula, would result in 1.3ºC of warming due to CO2 alone, and 2ºC of total warming, using the simple relationship that two-thirds of all greenhouse warming since 1750 is down to CO2, and the remainder is due to CH4, N2O and other trace gases.
(d) Diminishing impacts? Just reading off the chart, a further 50ppm rise to 500ppm raises temperature by 0.3ºC; a further 50ppm rise to 550ppm raises temperature by 0.27ºC; a further 50ppm rise to 600ppm raises temperature by 0.25ºC; and a further 50ppm rise to 650ppm raises temperature by 0.23ºC. The point is that rising atmospheric CO2 also raises global temperature along with it. While it is true that each incremental 50ppm has less impact than the prior 50ppm, the pace of the slowdown is itself quite slow, and not enough to dispel our ultimate need to decarbonize.
(e) There is a theoretical levelling off point due to the log relationship, where incremental CO2 makes effectively no difference to global temperatures, but from the equations above, it is so far in the future as to be irrelevant to practical discussions about decarbonization: it is probably somewhere after atmospheric CO2 has surpassed 4,000 ppm and CO2 has directly induced about 8C of warming.
In conclusion, the simple formulae that we have reviewed suggest that the ‘budget’ for 2ºC of total global warming is reached at a total atmospheric CO2 concentration of 450ppm. Of the budget, about two-thirds is eaten up by CO2, and the remaining one-third is from other anthropogenic greenhouse gases, mainly methane and N2O. This is what goes into our climate modelling, and why we think it is also important to mitigate methane emissions and N2O emissions from activities such as crop production.
(5) Controversies: challenges for simple CO2-warming equations?
Welcome to the section of this short note that is probably going to get controversial. Our intention is not to inflame or enrage anybody here. But we are simply trying to weigh the evidence objectively.
(a) Gamma uncertainty. Our simple climate formula above used a gamma value of 0.5ºC per W/m2 of radiative forcing. The IPCC has said in the past that this is a good average estimate, and that its gamma value has an uncertainty range of +/- 20%. Even this would be quite uncertain. For example, it means that the CO2 budget for 2ºC of total warming would be anywhere between 420-510ppm of atmospheric CO2, using the formulae above.
(b) More gamma uncertainty. Worse, some sources that have crossed our screens have suggested gamma values as low as 0.31ºC per W/m2 of radiative forcing, and others as high as 0.9ºC per W/m2 of radiative forcing. One of the key uncertainties seems to be around interaction effects and feedback loops. For example, a warmer atmosphere can store more water vapor. And water vapor is itself a greenhouse gas.
(c) What percentage of CO2 emitted by human activities remains in the atmosphere and what percent is absorbed by the oceans? We have assumed almost no incremental CO2 emitted by human activities is absorbed in the oceans, and almost all remains in the atmosphere, in our simple climate model.
(d) Other variables. Our model does not factor in the impacts of other variables that have an impact on climate, such as Milankovitch cycles, solar cycles, ocean currents, massive volcanic eruptions or mysterious Dansgaard-Oeschger events. (And no doubt there are some super-nerdy details of climate science that are not yet fully understood. But surely that does not invalidate the basics. While I may not fully grasp the Higgs-Boson, I still try to avoid cycling into large and immovable obstacles).
(e) We have over-simplified radiative forcing. There is no single formula that perfectly sums up the impact of CO2 on climate, because the Earth is not a single, homogenous disc, pointed directly at the sun. Some of these over-simplifications are obvious. Others are more nuanced. Clouds reduce the mean radiative forcing due to CO2 by about 15%. And the impacts of different gases can be different across vertical profiles through the atmosphere, for example, stratospheric adjustments reduce the impact of CO2 by 15%, compared to a perfectly mixed and homogenous atmosphere.
(f) Warming to-date. Perhaps most controversially, our simple formulae discussed above suggest that with atmospheric CO2 at 415 ppm and a gamma value of 0.5ºC, the world should already be 1.1ºC warmer than pre-industrial times due to CO2 alone, and this equates to being around 1.6ºC warmer than pre-industrial times due to a combination of all greenhouse gases. In contrast, the world currently appears to be around 1.1ºC warmer, in total, than it was in pre-industrial times according to the data below. This may mean that our gamma value is too high, or that our formulas are too conservative. Or conversely, it could simply mean that there are time lags between CO2 rising and temperature following. We do not know the answer here, which is unsatisfying.
Conclusions: what is the relationship between CO2 and warming?
How does CO2 increase global temperature? The advantages of simple formulae are that they are simple and can be used to inform our models. The disadvantages are that the global energy-climate system is complex, and will never be captured entirely by simple formulae.
Our aim in this short note is to explain the formulas that we are using in our energy-climate models and in our roadmap to net zero. We think it is possible to stabilize atmospheric CO2 at 450ppm, by reaching ‘net zero’ around 2050, in an integrated roadmap that costs $40/ton of CO2 abated; and reaches an important re-balancing between human activities and the natural world.
450ppm of atmospheric CO2 is possibly a conservative budget. There may be reasons to hope that true ‘gamma’ values for global warming, or forcing co-efficients, are lower than we have modelled. But it makes sense to ‘plan for the worst, hope for the best’. And regardless of specific climate-modelling parameters, it makes sense for a research firm to look for the best combination of economics, practicality, morality and opportunity in the energy transition.