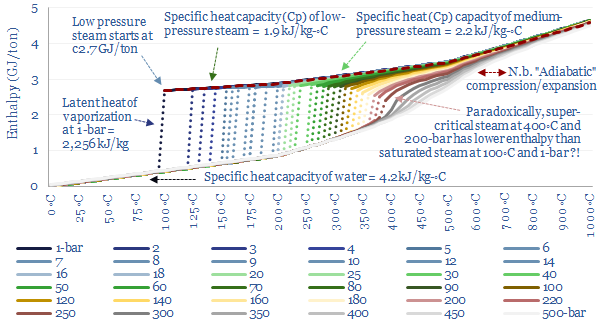
This data-file quantifies the energy needed to produce steam, for industrial heat, power, chemicals, CCS plants and hydrogen reforming. As rules of thumb, low pressure saturated steam at 100◦C requires 2.6 GJ/ton (720kWh/ton), medium pressure dry steam at 6-bar and 300◦C requires 3 GJ/ton (830kWh/ton) and super-critical steam at 250-bar and 600◦C requires 4 GJ/ton (1,200kWh/ton).
Steam is used across dozens of industrial processes that have crossed our screens, from manufacturing, to steam cracking, to hydrogen reforming, to amine regeneration in CCS to nuclear power. This all raises the question of how much energy is needed to produce steam?
What is the energy content of steam at 1 atmosphere’s pressure?
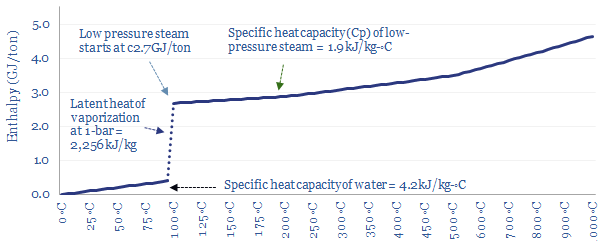
At a constant pressure of 1-bar (i.e., 1 atmosphere), it takes 4.2 kJ of energy to heat each kg of water by each 1◦C (aka the specific heat capacity of water). So it might require 0.34 GJ/ton of energy to heat 20◦C water up to a boiling point of 100◦C.
Saturation point? When water in the liquid phase reaches 100◦C it becomes saturated with heat, and rather than getting hotter, additional heat will vaporize the water into steam. The resultant steam is ‘saturated steam’ in the sense that it cannot get any hotter either, until all of the water has evaporated.
Vaporizing water into steam requires breaking the bonds that hold water molecules together as a liquid, the latent heat of vaporization, which is 2,256 kJ/kg, or translated into other units, 2.3 GJ/ton.
Only once all of the water has vaporized, yielding ‘dry steam’, can the temperature increase further. It takes 1.9 kJ to heat each kg of steam by each 1◦C (aka the specific heat capacity of steam, Cp). Thus the enthalpy per ton of 1-bar steam can be read off the chart below.
Units and conversions. 1 ton of steam is 1,000 kg. 1GJ is 1,000 MJ. And 1MJ is equivalent to 1,000 kJ or 0.278 kWh. For more conversions – including into tons of coal, mcf of gas, bbls of oil or alternatives such as mmbtu – please see our overview of energy units.
Amazingly, the discussion above shows that less than 20% of the thermal energy needed to make steam is the energy needed to bring room temperature water to the boil, and over 80% of the energy is needed to boil 100◦C water into 100◦C steam. This slow boiling behaviour is what allows you to cook pasta. Or at least this is the case at atmospheric pressure.
What is the energy content of pressurized steam?
The discussion above simplistically assumed 1-bar of pressure. In other words, it assumed that the steam can expand immediately when it is produced, into a wide open area.
In practice, industrial facilities will prefer to generate pressurized steam. Pressurized steam is more useful. It will naturally flow wherever you direct it, without needing to be compressed using a capex-intensive, maintenance intensive and energy-intensive compressor. But it also makes the energy economics more complicated.
Pressure changes water’s boiling point? When water boils into steam at 1-bar of pressure, then its volume naturally expands by 1,600x. Hence if the steam is held in a closed or semi-closed vessel, the pressure will naturally start to rise very significantly. In turn, as pressure rises, the saturation temperature for water also rises. The boiling point rises. At 100-bar (i.e., 100 atmospheres of pressure), water does not boil until 300◦C.
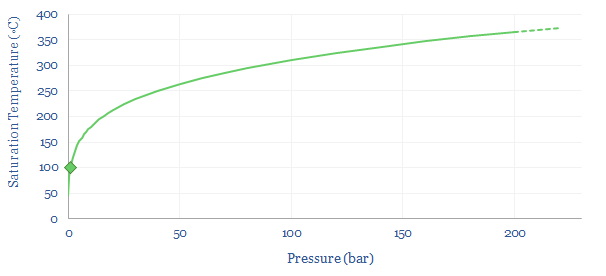
So how does this change the energy costs of making steam? You might intuitively think that it would require more energy to boil water into steam with higher temperature and pressure. But this is not entirely the case. When gases expand, they cool. And so the more they expand, the more energy must be added to heat them back up again to maintain the desired temperature. High pressure steam, by definition, has expanded less than low pressure steam. This is shown in the chart below. At 1-bar, boiling 100◦C water into 100◦C steam requires a 1,600x expansion. But boiling water at 100- bar and 500◦C only requires a 33x expansion. Generating higher density steam requires less energy to be added to ‘make up for’ the natural tendency of gases to cool down as they expand. So how can we quantify this effect?
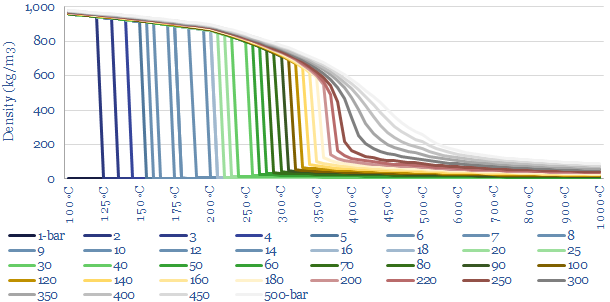
In energy terms, we can quantify how the latent heat of vaporization declines as pressure and temperature increase. At 1-bar of pressure, water boils at 100◦C, and this requires overcoming the latent heat of vaporization of water, of 2,256 kJ/kg, which is shown in the charts below as the difference between the green dot and the blue dot. But the chart also shows how the latent heat of vaporization decreases, at higher temperatures and pressures. There is ever more enthalpy in the water phase. And less energy must be re-added to compensate for the cooling effects of gas expansion.
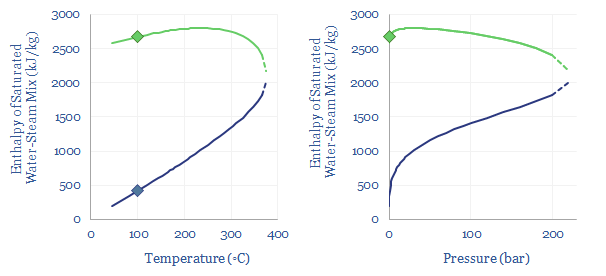
What is the critical point of steam? Ultimately, there is a point on the diagram, at 220-bar and 375◦C temperature where the latent heat of vaporization has fallen to zero. This is the ‘critical point’. At 220-bar of pressure and 375◦C temperature there is effectively no difference between steam and water. There is no sudden point of expansion! Just a very hot and dense soup of water particles. Supercritical fluids, which lie above their critical temperatures and pressures, can get hotter and denser than subcritical fluids, which is useful for efficient power generation.
The relationship between steam’s enthalpy and temperature is plotted below, this time with more sensitivity, ranging from 0-600◦C of temperature and 1-500 bars of pressure. The solid lines illustrate specific heat, where energy is added to the fluid mixture raising its enthalpy and its temperature. The dashed lines show the latent heat of vaporization for saturated steam, where further energy must be added to vaporize water, before the temperature can increase any further. And as noted above, the latent heat of vaporization becomes smaller and smaller at higher pressures and temperatures, up to the critical point, where the latent heat of vaporization is zero.
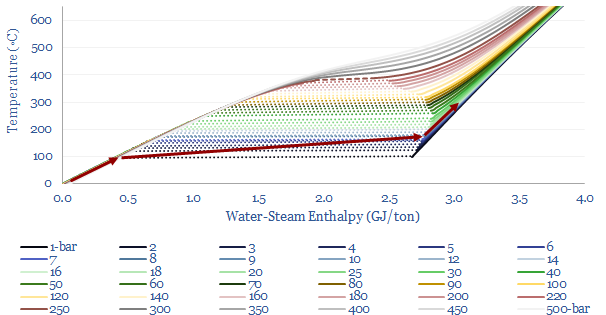
For a good rule of thumb, you can read off the enthalpy of steam from this chart, depending on its temperature and pressure.
You can also compare the energy content of steam at different temperatures and pressures using the chart above, to construct simple thermodynamic cycles. However, note that if you are comparing steams at different pressures, you must be careful to assume isentropic compressions and expansions! Let us unpack this idea in the next section.
How does entropy affect the energy content of steam?
An apparent paradox in the chart is that it seems to imply you could create and destroy energy, violating the laws of thermodynamics?!
For example, the chart shows there is no difference in the energy content between super-critical steam at 460◦C and 250-bar and medium-pressure steam at 280◦C and 10-bar. According to the chart, both of these steams would have the exact same enthalpy of 3.0 GJ/ton. How can this be? Does it really require NO incremental energy to take a 10-bar and 280◦C gas, compress it to 250-bar (requires work), and heat it to 460◦C (requires heat)?
Enthalpy versus entropy. These two steams in our example above, despite having the same enthalpy, have different entropies. Steam at 280◦C and 10-bar has an entropy level of 7.0 kJ/kg-K. Steam at 460◦C and 250-bar has an entropy level of 5.7 kJ/kg-K (chart below). The entropy of a system does not change unless heat flows in or out of the system. The concept of entropy is explained in more detail in our overview of thermodynamics.
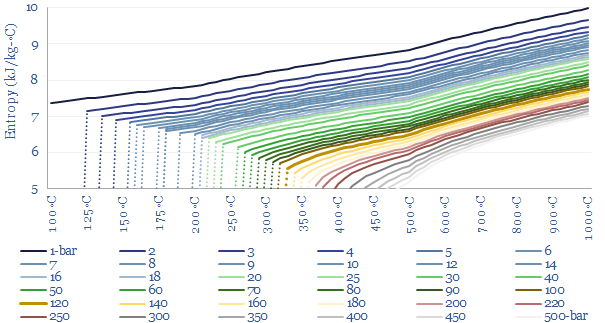
What this means in practice is that compressing a 280◦C gas stream from 10-bar to 250-bar — isentropically, i.e., without letting any heat transfer take place into or out of the steam — would absorb about 1.2 GJ/ton of compression work, and this would naturally tend to heat the steam up to about 850◦C. You can read this off the chart above by moving ‘left to right’ along the same horizontal line. This is simply how the gas laws go for steam. You could then extract useful heat from the steam as it cools back down to 460◦C, lowering both its enthalpy and its entropy. The enthalpy extracted would be, you guessed it, 1.2 GJ/ton. And if you later wanted to ‘get back’ to the starting point of 10-bar and 280◦C then ultimately you would need to flow heat energy into the system, to raise the entropy back to its original value. These values are simply read from the steam data tables compiled in this data-file.
In order to avoid violating the laws of thermodynamics, it is usually necessary to model compressions and expansions as being isentropic. Assume that heat energy cannot flow in or out of the system during the compression or expansion process, and thus that entropy remains constant. This is why we need steam tables, like the ones aggregated in this data-file, to show how actual energy flows will behave and quantify the energy needed to produce steam. The data-file captures density, volume, enthalpy, internal energy, PV energy and entropy at 100 x 40 different temperatures and pressures.
The data file is compiled in the way we find most useful for our own economic models and CO2 intensity calculations. Please see our primer for a more detailed overview of thermodynamics. The underlying source of the data is public disclosures from NIST.