This datafile calculates the semiconductor conductivity and semiconductor resistivity from first principles, based on their bandgap, doping, electron and hole mobility, temperature, the Fermi-Dirac distribution and the Effective Density of States. Put in any inputs you like to compute the resistance of silicon, germanium or GaAs.
The purpose of this data-file is to break down the conductivity of semiconductors, in spreadsheet format, from first principles, as a useful reference file for our broader modelling of semiconductors, from solar panels to electric vehicles.
The basic formula for conductivity in metals is that S=neμ, where n is the number of charge carriers (usually an integer multiple of the number of atoms), e is the fundamental energy of an electron (1.6 x 10^-19 Joules per electron) and μ is the mobility of the electrons in the material (maybe around 40cm2/V-s as a good ballpark for copper). Resistivity in Ohm-cm is simply 1 ÷ conductivity in Siemens per centimeter.
The formula for conductivity in semiconductors is more complex than metals, because the charge carriers may be conduction band electrons, valence band holes, donor electrons from pentavalent dopants or acceptor holes from trivalent dopants. But generally semiconductor conductivity: σ = ne e μe + np e μp, and these values are in the data-file.
For intrinsic semiconductors, the number of conduction band electrons must be computed as a function of the bandgap, Boltzmann’s constant, temperature and the Effective Density of States (Nc). That final term, in turn, is calculated by multiplying the Fermi-Dirac distribution by the Density of States function and then using calculus to find the ‘area under the curve’. It is all in the data-file.
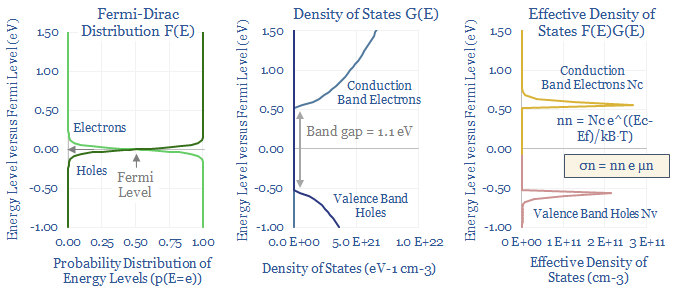
Undoped silicon (aka intrinsic silicon) will likely have an intrinsic resistivity of around 250,000Ω-cm at room temperature, of which 90% comes from the conductivity of conduction band electrons (rather than holes). There might be 5 x 10^22 silicon atoms per cm3, yielding 1.6 x 10^10 conduction band electrons per cm3, with an average mobility of 1,425 cm2/V-S. These numbers can all be flexed in the data-file.
Doping makes semiconductors an order of magnitude more conductive, and enables their assembly into devices such as light emitting diodes, transistors and solar cells. Moderately doped silicon might contain 1 impurity per 10^7 silicon atoms yielding 5 x 10^14 charge carriers per cm3 (table below). Each 10x increase in doping concentration generally improves conductivity by 10x.
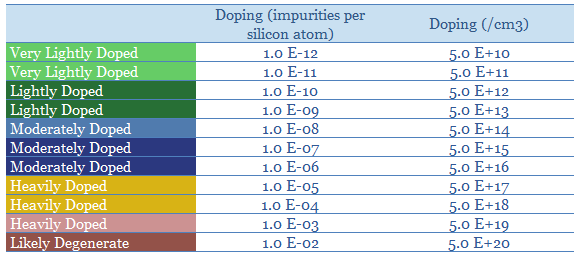
Although even a heavily doped semiconductor will still be about 500-5,000x more resistive than a conductive metal such as copper. Please download the data-file to stress test semiconductor conductivity and resistivity. More of the theory is explained in our overview of semiconductors.
