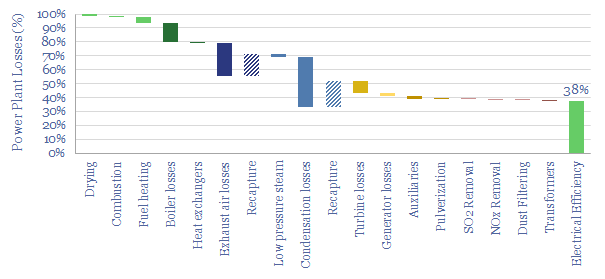
This data-file is a simple loss attribution for a thermal power plant. For example, a typical coal-fired power plant might achieve a primary efficiency of 38%, converting thermal energy in coal into electrical energy. Our loss attribution covers the other 62% using simple physics and industry average data-points.
In our power plant loss attribution, the largest losses are modeled to occur in the steam condensation stage of the Rankine Cycle (17% of losses), the boiler (14%), turbine losses (9%), heat lost in exhaust air (8%), fuel heating (4%), generator losses (2%), plant auxiliaries (2%), and other smaller losses, including incomplete combustion, fuel drying, fuel milling, flue gas desulfurization, NOx removal via selective catalytic reduction, dust removal via electrostatic precipitators and electrical losses such as transformers.
A range of typical efficiency factors are summarized from technical papers. But a reasonable base case might include 86% boiler efficiency, 90% turbine efficiency, 97% generator efficiency and 8.5% auxiliary losses (note the denominators differ case-by-case, as shown in the data-file).
Thermal power plant efficiency can vary from 20% to 50%. You can stress test different variables in rows 30-46, in order to test rules of thumb over the thermal efficiency of power plants.
Heat recovery. A massive 60% of a thermal power plant’s gross thermal energy ends up being imparted into hot exhaust gases from the boiler, and low pressure steam exiting a cascade of turbines. This is waste heat. The recapture of waste heat is the largest determinant of the efficiency of a thermal power plant. Our base case model assumes that 50% of the low-pressure steam heat and two-thirds of the exhaust gas waste heat is recaptured via heat-exchangers (e.g. warming up input air, fuel and cold water entering the boilers). Without this heat recovery, the thermal efficiency of our coal-fired power plant would be a pathetic 3%. And indeed, sub-10% efficiency factors were common from the dawn of the industrial revolution through to the start of the 20th century (data here). A 10pp increase in heat recovery raises our efficiency factor by 3% from 38% to 41%. However, in practice, this will also require higher capex.
Unit efficiency. Efficiency can be uplifted by around 4%, to 42%, by replacing average boilers, turbines, generators and auxiliary loads with best-in-class boiler efficiency, turbine efficiency, generator efficiency and auxiliary loads. However, in practice, this will also require higher capex.
Hotter cycles. Our base case model is a supercritical cycle around 566◦C, however, varying the maximum temperature of the cycle by +/- 100◦C changes the cycle efficiency by +/- 1%. The reason is that less working fluid is needed for a hotter cycle, which lowers the losses involved in evaporating and then re-condensing water; there is simply less water.
Hotter ambient temperatures. Our base case model assumes an ambient temperature of 20◦C. However, when ambient temperatures are 40◦C, efficiency falls by 0.3%, because it becomes harder to extract as much heat from the working fluid as it expands across the turbines and in the process cools towards ambient temperatures.
Higher-grade fuel. Coal grades vary. But generally, coal needs to be heated to above 400◦C to ignite, and above 500◦C to auto-ignite (data here). Replacing high-grade bituminous coal (6,500 kWh/ton) with low-grade lignite (3,500 kWh/ton) will lower efficiency by around 3%, because of the additional fuel-heating that is required.
Wetter fuel. Similar rules apply to fuels with a higher moisture content, as this moisture needs to be evaporated. Our base case coal has 10% moisture content, whereas coal with 20% moisture content will lower efficiency by 0.3%.
Exhaust gas regulations. We think that 1.3% of the plant’s electricity will be lost in meeting developed world flue gas regulations, which require SO2 removal via flue gas desulfurization, NOx removal via selective catalytic reduction and dust removal via electrostatic precipitators. However, some thermal coal plants do not face exhaust gas regulations. Others face even more stringent regulations.
Biomass fired power. We have also developed a biomass-fired variant of the model, reflecting the lower thermal energy of wood versus coal, the higher moisture content and a lower combustion temperature. The base case thermal efficiency of a wood-fired power plant is 34%.
Gas turbines. We have also developed a gas-turbine variant of the model, reflecting the energy economics of the Brayton cycle from first principles, as a function of compression ratios and temperatures across the cycle. The base case thermal efficiency is 40% for a simple cycle gas turbine, rising to 57% efficiency for a combined cycle gas turbine (chart below). Here is hoping that this simple model of gas turbine efficiency is useful. Intriguingly, we think that the energy penalties for gas-fired CCS are only around 10-20%, versus 40% for CCS at power plants combusting solid fuels. For simple cycle gas turbines, the amine reboiler duty can often be met entirely via waste heat.
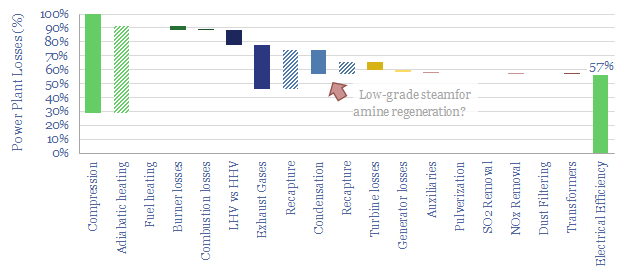
All of the variables above can be stress-tested in the data-file, which serves as a simple power plant loss attribution. The discussion above highlights that thermal power plants can have efficiencies anywhere from 20-60% depending on their configuration.