This data-file aggregates important thermodynamic properties of CO2 at different temperatures and pressures. Specifically, how do different pressures and temperatures dictate CO2’s density, Cp, Cv, Heat Capacity Ratio (gamma), Entropy, and Compressibility. These variables matter for CO2 compression, CCS and sCO2 power cycles.
Our overview of compressors shows how the energy needed to compress a gas varies as a function of its temperature, compressibility, heat capacity ratio (Cp/Cv) and its molar mass.
Our overview of thermodynamics explains how the efficiency of a gas-fired power cycle (i.e., a Brayton cycle) depends on the ability to heat gases to high temperatures and achieve high compression ratios (in turn, a function of Cp/Cv, compressibility, etc).
Hence what are the thermodynamic properties of CO2 at different temperatures and pressures? This data-file aims to aggregate some data in a user-friendly format.
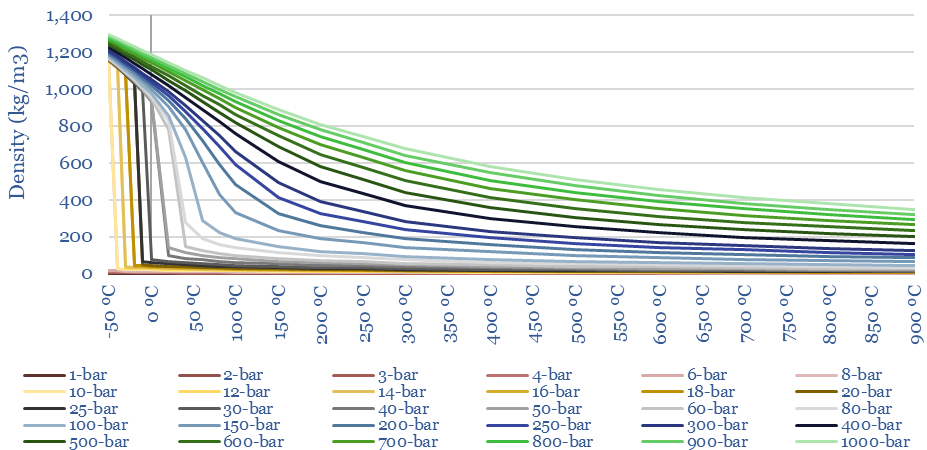
The density of CO2 at different temperatures and pressures is plotted below. Liquefied CO2 will be in the range of 1,000-1,200kg/m3, which is over 2x more dense than LNG. Moreover, the density of heated CO2 at 300-bar and 600C is 170kg/m3, which is 2x higher than the equivalent density of steam. This explains why CO2 can be an interesting working fluid for decarbonized gas power (e.g., the NET Power cycle), because higher densities mean small plant sizes.
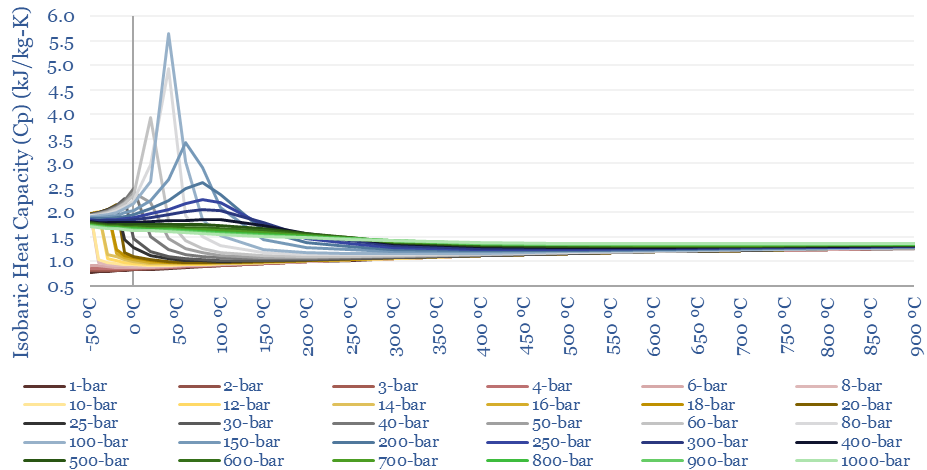
The isobaric heat capacity of CO2 (Cp) at different temperatures and pressures is plotted below. This is a truly strange graph, with Cp fluctuating wildly at low-intermediate temperatures. This has a strange result for heating CO2 in a heat exchanger. As energy is transferred from a hot CO2 stream to a cold CO2 stream, temperatures will drop 1.5x faster on the hot side than they rise on the cold side. In other words, it can be quite challenging to heat exchange CO2 compared to other gases.
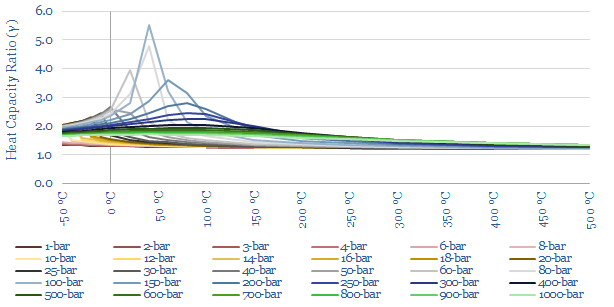
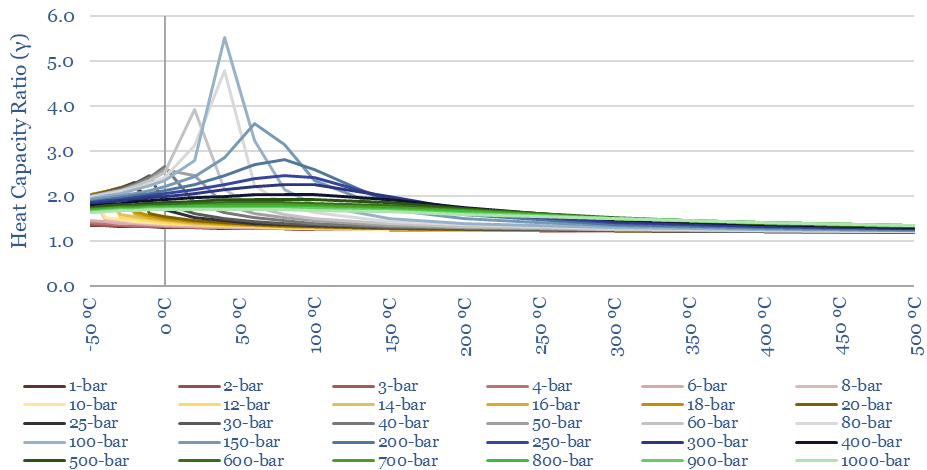
The heat capacity ratio of CO2 (gamma = Cp/Cv) at different temperatures and pressures is plotted below. Fluctuations in gamma follow from fluctuations in Cp (above). The energy needed to compress a gas rises with heat capacity ratio. This shows that it is quite easy to compress CO2 to liquefaction temperatures (around 6-10 bar is envisaged for CO2 trucking or CO2 shipping). But there are some unexpected spikes in the heat capacity ratio in the ranges relevant to CO2 pipelines (100-bar) and CO2 gas turbines (300-bar).
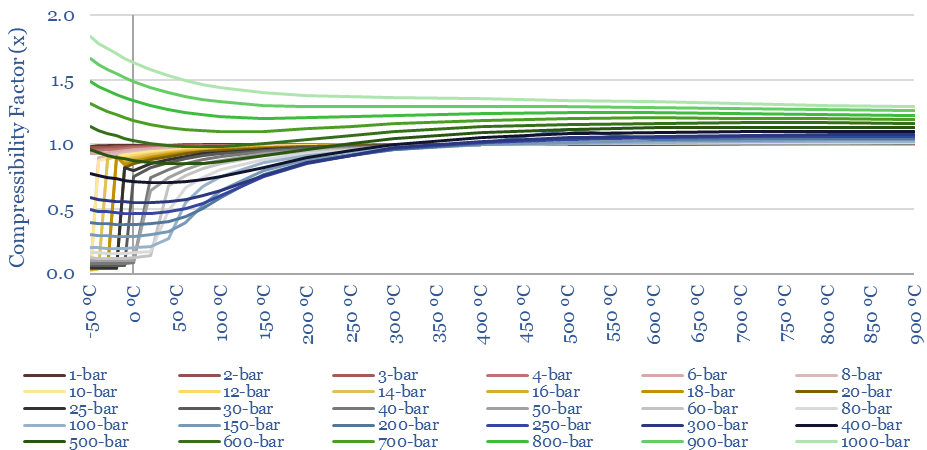
The compressibility of CO2 at different temperatures and pressures is plotted below (Z factor). More energy is required to compress gases with higher compressibility (linear relationship). What is interesting about CO2 is the wide variability in its compressibility. Compared to air, it is easier to compress at low temperatures and intermediate pressures.
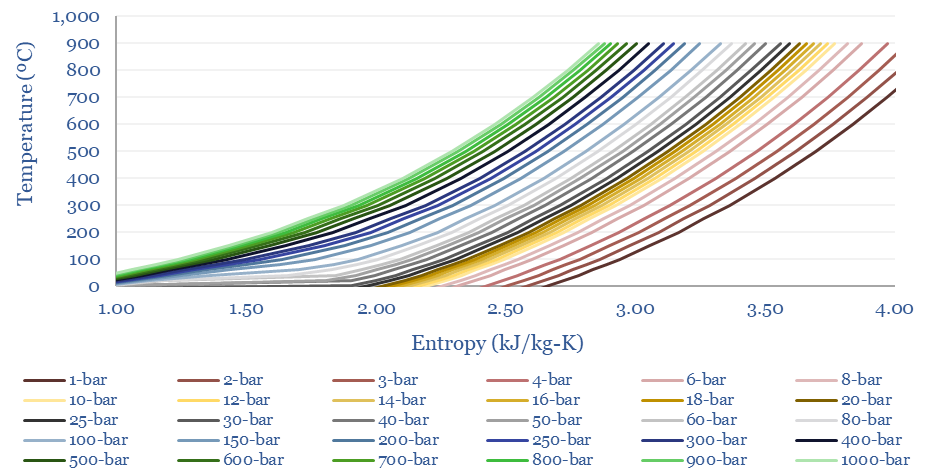
The entropy of CO2 at different temperatures and pressures is plotted below. As a rule of thumb, the entropy of CO2 is around one half the entropy of air and steam, at comparable pressures and temperatures. This also helps the efficiency of CO2 power cycles.
Underlying data on the thermodynamic properties of CO2 at different temperatures and pressures are presented in a user-friendly format in this data-file.