Computation, the internet and AI are inextricably linked to energy. Information processing literally is an energy flow. Computation is energy. This note explains the physics, from Maxwell’s demon, to the entropy of information, to the efficiency of computers.
Maxwell’s demon: information and energy?
James Clark Maxwell is one of the founding fathers of modern physics, famous for unifying the equations of electromagnetism. In 1867, Maxwell envisaged a thought experiment that could seemingly violate the laws of thermodynamics.
As a starting point, recall that a gas at, say 300ºK does not contain an even mixture of particles at the exact same velocities, but a distribution of particle speeds, as given by the Maxwell-Boltzmann equations below.
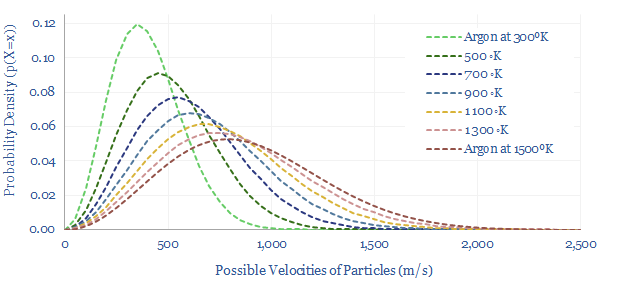
Now imagine a closed compartment of gas molecules, partitioned into two halves, separated by a trap door. Above the trap door, sits a tiny demon, who can perceive the motion of the gas molecules.
Whenever a fast-moving molecule approaches the trap door from the left, he opens it. Whenever a slow-moving molecules approaches the trap door from the right, he opens it. At all other times, the trap door is closed.
The result is that over time, the demon sort the molecules. The left-hand side contains only slow-moving molecules (cold gas). The right-hand side contains only fast-moving molecules (hot gas).
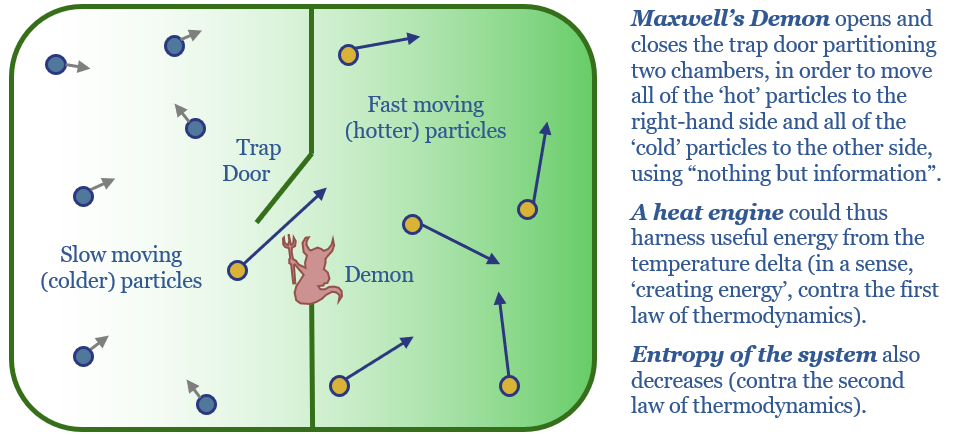
This seems to violate the first law of thermodynamics, which says that energy cannot be created or destroyed. Useful energy could be extracted by moving heat from the right-hand side to the left-hand side. Thus in a loose sense the demon has ‘created energy’.
It also definitely violates the second law of thermodynamics, which says that entropy always increases in a closed system. The compartment is a closed system. But there is categorically less entropy in the well-sorted system with hot gas on the right and cold gas on the left.
The laws of thermodynamics are inviolable. So clearly there must be some work done on the system, with a corresponding decrease in entropy, by the information processing that Maxwell’s demon has performed.
This suggests that information processing is linked to energy. This point is also front-and-center in 2024, due to the energy demands of AI.
Landauer’s principle: forgetting 1 bit requires >0.018 eV
The mathematical definition of entropy is S = kb ln X, where kb is Boltzmann’s constant (1.381 x 10^-23 J/K) and X is the number of possible microstates of a system.
Hence if you think about the smallest possible transistor in the memory of a computer, which is capable of encoding a zero or a one, then you could say that it has two possible micro-states, and entropy of kb ln (2).
But as soon as our transistor encodes a value (e.g., 1), then it only has 1 possible microstate. ln(1) = 0. Therefore its entropy has fallen by kb ln (2). When entropy decreases in thermodynamics, heat is usually transferred.
Conversely, when our transistor irreversibly ‘forgets’ the value it has encoded, its entropy jumps from zero back to kb ln (2). When entropy increases in thermodynamics, then heat usually needs to be transferred.
You see this in the charts below, which plots the PV-TS plot for a Brayton cycle heat engine that harnesses net work via moving heat from a hot source to a cold sink. Although really an information processor functions more like a heat pump, i.e., a heat engine in reverse. It absorbs net work as it moves heat from an ambient source to a hot sink.
In conclusion, you can think about the encoding and forgetting a bit of information as a kind of thermodynamic cycle, as energy is transferred to perform computation.
The absolute minimum amount of energy that is dissipated is kb T ln (2). At room temperature (i.e., 300ºK), we can plug in Boltzmann’s constant, and derive a minimum computational energy of 2.9 x 10^-21 J per bit of information processing, or in other words 0.018 eV.
This is Landauer’s limit. It might all sound theoretical, but it has actually been demonstrated repeatedly in lab-scale studies: when 1 bit of information is erased, a small amount of heat is released.
How efficient are today’s best supercomputers?
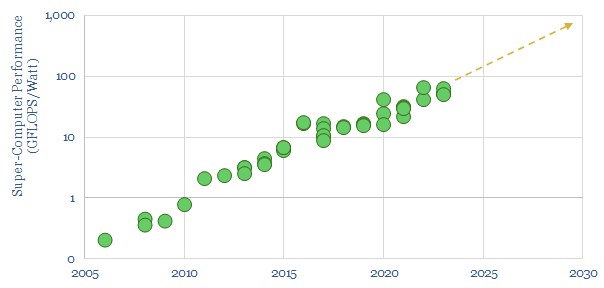
The best super-computers today are reaching computational efficiencies of 50GFLOPS per Watt (chart below). If we assume 32 bit precision per float, then this equates to an energy consumption of 6 x 10^-13 Joules per bit.
In other words, a modern computer is using 200M times more energy than the thermodynamic minimum. Maybe a standard computer uses 1bn times more energy than the thermodynamic minimum.
One reason, of course, is that modern computers flow electricity through semiconductors, which are highly resistive. Indeed, undoped silicon is 100bn times more resistive than copper. For redundancy’s sake, there is also a much larger amount of charge flowing per bit per transistor than just a single electron.
But we can conclude that information processing is energy transfer. Computation is energy flow.
As a final thought, the entirety of the universe is a progression from a singularity of infinite energy density and low entropy (at the Big Bang) to zero energy density and maximum entropy in around 10^23 years from now. The end of the universe is literally the point of maximum entropy. Which means that no information can remain encoded.
There is something poetic, at least to an energy analyst, in the idea that “the universe isn’t over until all information and memories have been forgotten”.
