How do we quantify the minimum energy needed to heat materials and melt materials? This data-file calculates values, in kWh/ton, from first principles, based on target temperatures, specific heat capacities and latent heat capacities. A good rule of thumb is 25 kWh of useful energy to heat each ton of material by each 100ºC.
(1) Thermodynamics 101. Heating and melting materials requires energy, inducing particles to vibrate more (specific heat) and ultimately to break the bonds that hold them together as a solid or liquid (latent heat). By definition. 1 Joule can be defined as the specific heat energy needed to raise the temperature of 1 gram of air by 1ºC (see our note on energy units and conversions).
(2) Advanced thermodynamics. If you really want to get into the weeds, and quantify the minimum energy needed to heat, melt and vaporize different materials, you will find yourself entering the murky world of quantum physics. For example, the specific heat of different materials can be approximated using the well known Dulong-Petit Law. But different materials’ specific heat capacity values are not actually ‘constant’. They rise with temperature, as higher-energy particles suddenly gain the ability to spin in novel ways, requiring ever more complex physics, such as the Einstein photo-electron model. But we can ignore all of this for now.
(3) Heating a material makes it hotter. We all use this principle every day. For example, the “perfect bath” contains about 100L of water (or 0.1 tons) at 40ºC. If it is 15ºC outside, then this requires 25ºC of heating, at 4.2 J/gºC, or 10MJ of useful energy, aka 2.8 kWh of useful energy. This is the thermodynamic minimum useful energy. Including the losses in a boiler, the unintended heating of pipes and surroundings, a bath probably requires around 4kWh of input energy (conclusion: Europeans may need to take fewer baths in winter-2022).
(4) Industrial heat differs in that the volumes are larger and the temperatures are hotter. But a good rule of thumb is that heating each ton of material by each 100ºC requires a minimum of around 25kWh of useful energy. The numbers can vary widely, however.
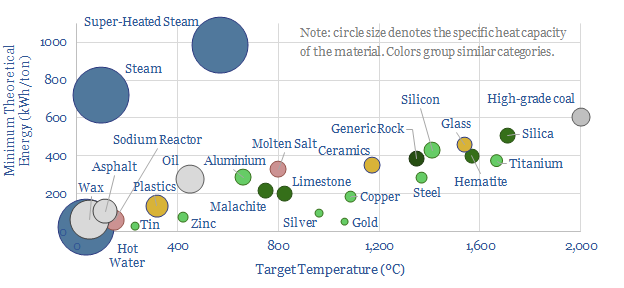
(5) Melting metals is necessary before they can be forged or shaped. This is represented by the green dots in our chart above. Generally, metals have relatively low specific heat capacities, around 0.4 J/gºC. This is literally 10x less than water. It varies by metal. But this shows that for many metals, the energy intensive step may not be melting and working the metal, but smelting it in the first place. For more details, please see our metals research.
(6) Manufacturing heat examples. Calcium carbonate is thermally decomposed at 825ºC as an input to making cement. Ceramics are fired at 1,200ºC. Glass is produced at 1,500ºC. The minimum energy consumption here is 200-500kWh/ton. But the real-world numbers can be 2-5x higher again. For example, it is not enough to heat ceramics up in a kiln. You also have to keep the kiln hot for 10-20 hours. This is why we need to tackle total energy consumption of different products, case by case, across our c150 economic models.
(7) Mining efficiency. Mined materials are going to be crucial to the energy transition. But mining is energy intensive. And so this requires a focus on improving mining efficiency. You could argue therefore that flotation and leaching are two of the most important energy saving technologies in the future of the world. If you can concentrate ores before smelting or refining them, then you do not have to pointlessly heat up non-valuable co-associated rocks, which requires 400 kWh/ton to reach an average temperature of 1,350ºC.
(8) Silicon stands out for its ridiculously high energy intensity. We think that making solar PV silicon requires over 80,000 kWh/ton, and it is one of the most energy intensive materials we have ever looked at. The first step is melting sand at 1,700ºC (500 kWh/ton). Then there are multiple steps of re-crystallizing and then re-melting the silicon, as described in our note here. Some of these steps grow crystals very slowly, at 10-20 nm per minute, and thus they take 80 – 110 hours, with temperatures in the range of 600-1,100ºC.
(9) Fuels. If you consider that oil refining requires heating crude oils to 400-500ºC, this is going to eat up a minimum of 275 kWh/ton, equivalent to 2% of the energy in crude oil in the first place, which is why oil refining dominates the Scope 1&2 CO2 intensity of oil products, hammers oil’s EROEI, and could be enormously improved by emulating the mining industry with non-thermal separation technologies. Likewise, the energy needed to heat up coal to its maximum combustion temperature of 2,000ºC is around 600kWh/ton, or around 10% of the energy in coal in the first place, and this is going to hurt efficiency, especially from lower grade coals. Because of the constant removal of hot ashes, it is inherently harder to capture the heat from coal compared with the heat from gas. And finally, the ridiculously high energy footprint of steam — see below — explains the very high CO2 intensity of SAGD oil sands.
(10) Water and steam are weird. Finally, we should return to water. Water is weird. Water molecules love sticking together as a liquid. Their latent heat of evaporation is 2,250 J/g, which is 5x more than the next-closest material in our data-file. In other words, it takes 7x more energy to turn 100ºC water into steam than it took to bring 20ºC water up to 100ºC in the first place. This is also the reason that water will “boil” in a saucepan for long enough to make spaghetti carbonara, rather than suddenly vanishing into a particularly steamy kitchen. But the upshot is that turbines using water as a working fluid must work very hard to capture all of the energy from steam. In turn this underpins combined cycle gas turbines, combined heat and power, EGRs, and even next generation combustion technologies based around super-critical CO2, and next-generation nuclear using molten sodium or salt.
Further data on the energy needed to heat materials is broken down in the data-file, along with our underlying calculations.