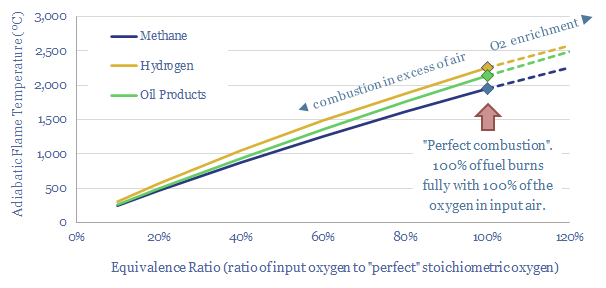
This data-file is a simple model calculating adiabatic flame temperatures from first principles. At an idealized, 100% stoichiometric ratio, the adiabatic flame temperature for natural gas is 1,960ºC, hydrogen burns 300ºC hotter at 2,250ºC and oil products burn somewhere in between, at around 2,150ºC. However, the calculations also show why hydrogen cannot always be dropped into an existing turbine or heat engine that was previously designed to run on other hydrocarbons.
What is adiabatic flame temperature?
Adiabatic flame temperature denotes the maximum theoretical temperature that can be reached by a mixture of gases during combustion, if precisely all of the enthalpy of combustion (in kJ/mol) is transferred directly into those gases.
Hence adiabatic flame temperature can easily be calculated from first principles, as a function of (a) the different input gases; (b) the resultant exhaust gases; (c) the masses of those gases (in kg); and (d) the specific heat capacity of each gas (Cp), which is the amount of energy needed to raise its temperature by 1-degree (in kJ/kg-K).
A 100% equivalence ratio denotes the condition where 100% of a fuel combusts perfectly and reacts with 100% of the oxygen in the input mixture. This 100% stoichiometry will naturally maximize the temperature of the resultant flame, because no heat is dissipated unnecessarily in heating up superfluous oxygen.
The data-file shows that at an idealized, 100% stoichiometric ratio, the adiabatic flame temperature for natural gas is around 1,960ºC, hydrogen burns 300ºC hotter at 2,250ºC and oil products burn somewhere in between, at around 2,150ºC. Satisfyingly, these bottom-up calculations match the widely quoted adiabatic flame temperatures shown in online resources such as Wikipedia.
Why does adiabatic flame temperature matter in industry?
Very hot process temperatures are needed for producing many metals, materials and in some hydrogen reforming reactors.
For example, a blast furnace can reach 1,100-1,600ºC. Cement plants decompose CaCO3 into clinker at 1,400-1,500ºC. Mined lithium ores are roasted at 1,100ºC to change the crystal structures of spodumenes. In semiconductor, mono-crystalline polysilicon for chips and solar panels is grown via the Czochralksi method at 1,425ºC; while the SiC used in cutting edge EV power-MOFSETs is grown at 2,000ºC in the Lely process. The heating-melting temperatures of different solids are compared here.
Reaching these very hot process temperatures requires a materially hotter flame temperature. You clearly cannot heat a process to 1,500ºC with a 1,000ºC flame.
Real world flame temperatures will tend to be lower than the adiabatic flame temperatures at 100% equivalent ratios, quoted above for methane, hydrogen and oil products.
Real world processes are not adiabatic. An adiabatic process is one where no energy is transferred in or out of the system. But in the real world, the entire point of generating heat is to transfer it out of the system and do some useful work, for example by driving a turbine or supplying energy into an endothermic chemical reaction.
Some combustion enthalpy will always be lost to heating the surrounding reactor/plant, reagents, and leaked into the surroundings.
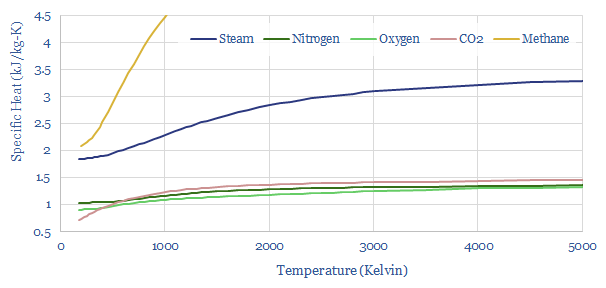
We used Cp as our specific heat capacity, which reflects the fact that some of the combustion enthalpy is expended in expanding the gases rather than just heating them up. Cp values rise with temperature. It gets incrementally harder to heat up hot gases (chart below).
Finally, in the real world, it is not recommended to fire a combustion reactor too close to 100% stoichiometry, otherwise the result may be incomplete combustion forming soots, carbon monoxide and nasty NOXs.
So in practice, if you are going to run a reactor with 1.5-2x the stoichiometric minimum oxygen content, as a margin of safety against incomplete combustion, in a real-world plant with heat losses, it can be challenging to achieve >1,000ºC process temperatures by burning fuels like natural gas, oil products or coal in an atmosphere of air (chart below).
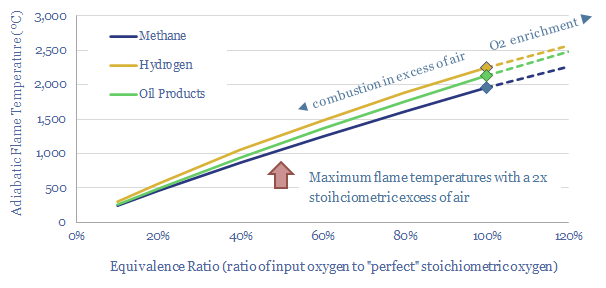
Achieving very high process temperatures often requires enriching fossil-fired combustion processes with additional oxygen beyond the 21% molar fraction found in air.
This need for super-high process temperatures is a key driver behind global industry’s 400MTpa oxygen demand, per our note below.
Flame temperature: can you blend hydrogen into existing heat engines?
The analysis of adiabatic flame temperature also shows why hydrogen cannot always be blended into pre-existing turbines or engines that were intended to be run on some different hydrocarbon, without some important engineering considerations.
For example, consider a gas turbine that has been designed to burn a mixture of 4-6% methane and 94-96% air, which equates to a 67-150% stoichiometric excess of oxygen, yields a maximum flame temperature around 900-1,250ºC, and an exhaust gas with around 4-6% CO2 concentration (calculations in the data-file).
Well, replace the 6% methane input with a 6% hydrogen input, and the adiabatic flame temperature only reaches about 450ºC. The reason is that each mol of hydrogen only releases one-third of the combustion enthalpy as each mol of methane (numbers in the file). All else equal, this lower temperature would detract over 20% from the energy efficiency of a typical Brayton Cycle. Oh dear.
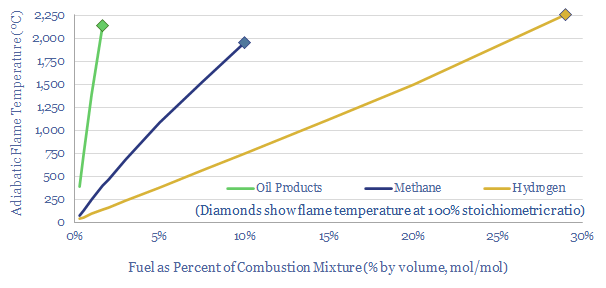
You could increase the temperature back to the original 1,250ºC target by mixing a 3x higher blend of hydrogen into the input gases. But now there are questions about whether the inlets can flow these higher volumes of fuel gas, whether the gases will mix evenly; or conversely, will there be localized hotspots with annoying consequences like melting your burner tips, or other parts of your plant.
Likewise an engine burning liquid hydrocarbons might only be spraying a mist of 0.5-1% oil products by volume into a combustion cylinder before ignition at 700-1,400ºC, according to these adiabatic flame temperature calculations.
If hydrogen is used as a combustion fuel, it will result in materially higher volumetric flow rates to generate the same temperatures as natural gas or liquid hydrocarbons.
When burned at its optical stoichiometric ratio, hydrogen will also yield 300ºC higher temperatures than burning methane. This can be a blessing in terms of thermodynamic efficiency. But conversely, the limit on pre-existing gas turbines is not the ability to generate high flame temperatures. It is the ability to withstand them! For example, via the temperature resiliency of cutting-edge super-alloys. And this is a key reason why gas turbines tend to flow excess air as coolant or re-circulate exhaust gases.
To control a process temperature, while blending in varying molar fractions of hydrogen, requires careful calculation. More hydrogen means more demand for engineering services, in our view.