What determines the Voltage of an electrochemical cell, such as a lithium ion battery, redox flow battery, a hydrogen fuel cell, an electrolyser or an electrowinning plant? This note explains electrochemical voltages, from first principles, starting with Standard Potentials and working through the Nernst Equation.
Redox Chemistry 101
Reducing agents. Some atoms “really want” to surrender unstable outer electrons and oxidize into positively charged ions. Lithium metal, for example, is so desperate to shed an outer electron that it will rip water apart, forming LiOH (Li+ and OH-) and H2 gas. This makes lithium metal a strong reducing agent. As it oxidizes, another atom must reduce.
Oxidizing agents. Other atoms “really want” to complete incomplete outer electron shells, gain electrons and thus “reduce” into negatively charged ions (or form covalent bonds). Oxygen, for example, is quite keen to accept electrons from metal atoms. So much so that ‘oxidation’ is named after it. As oxygen reduces, another atom must oxidize.
What is Standard Potential?
Standard Potential aims to quantify how much an atom wants to oxidize or reduce relative to the H2/H+ redox pair and measured in Volts. This sentence sounds confusing. But bear with us!
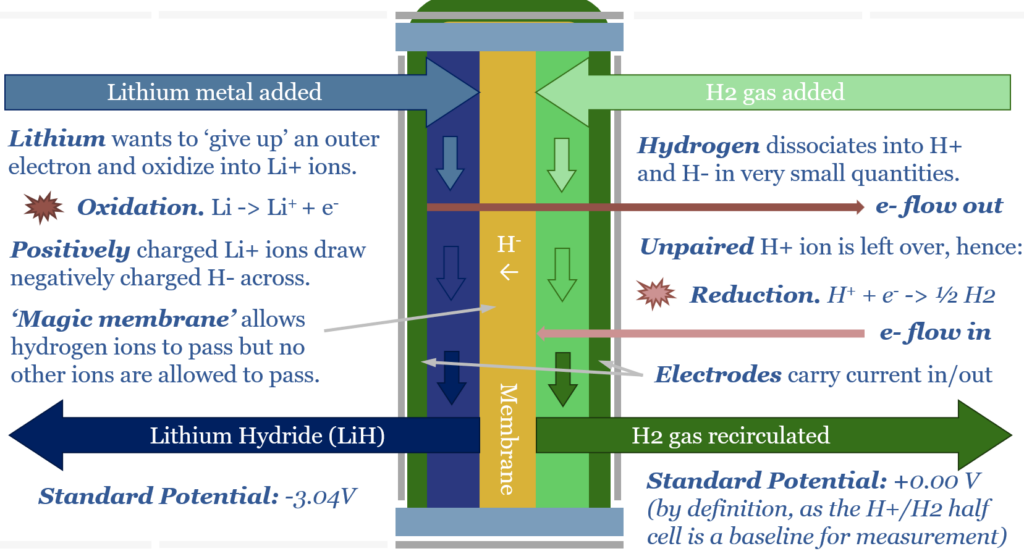
How should I think about standard potential? Imagine a magic electrochemical cell, with two electrodes, in two chambers, separated by a magical membrane. The key facet of this magic membrane is that ONLY H+ ions can cross the cell. On one side of the cell is a chamber of H2 gas. At any point in time, a very small portion of H2 gas is prone to dissociating into H+ and H- cations and anions. H2 <=> H+ + H- On the other side of the cell, we can add literally any reagent.
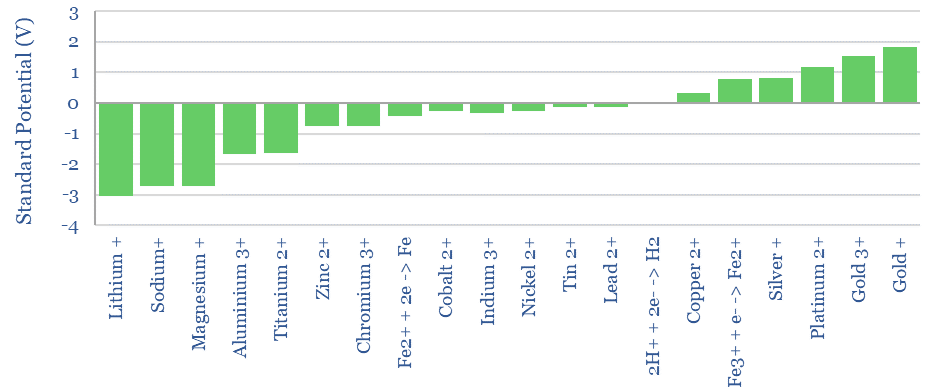
For example, if we add lithium to the other side of the cell, it will oxidize, surrendering an electron into an electrode, forming Li+. The Li+ will attract H- anions across the cell membrane to form LiH. This leaves an excess of H+ ions on the H-side of the cell. These H+ cations reduce, accepting an electron from a second electrode, and re-forming H2 gas. The chemical reaction is Li + H+ -> Li+ 0.5 H2. The thermodynamic result is that energy has been released by this reaction. The energy is imparted to the electrons that were ‘pushed out’ from the Li-side of the cell. Remember that 1 Volt simply means 1 Joule of energy per Coulomb of charge, where the elementary charge of 1 electron is 1.602×10^-19. Power = Voltage x Current. Hence our electrochemical cell is a power source, flowing a current (in Coulombs per second) with a voltage (in Joules/Coulomb). Lithium is one of the strongest reducing agents in chemistry with a Standard Potential of -3.04 Volts (relative to the H2/H+ redox pair).
As another example, if we add Fluorine gas to the other side of the cell, it will reduce, pulling in an electron from the first electrode. The chemical reaction is F2 + 2e -> 2F-. The F- ions will attract H+ cations across the cell membrane to form HF. This leaves an excess of H- anions on the H-side of the cell. These H- anions oxidize, surrendering an electron from the second electrode, reforming H2 gas. The chemical reaction is F2 + H2 -> 2HF. The thermodynamic result is that energy has been released by this reaction. The energy is imparted to the electrons that were ‘pushed out’ from the H-side of the cell. Fluorine is one of the strongest oxidizing agents in chemistry with a Standard Potential of +2.86 Volts (relative to the H2/H+ redox pair).
Redox flow batteries are very similar to these idealized electrochemical cells. The example below uses Vanadium, in V2+, V3+, V4+ and V5+ oxidation states.
Batteries are Electrochemical Cells
All batteries work via this same redox chemistry principles that were illustrated above. And the standard potentials of each half-cell add together to yield the standard potential of the battery.
For example, imagine an electrochemical cell with Li metal on one side, F2 gas on the other, and a membrane that was ONLY permeable to Li+ ions. On the F-side of the cell, F will reduce to F-, with a Standard Potential of +2.86V. On the Li-side of the cell, Li will oxidize into Li+, with a Standard Potential of -3.04V. The resultant Li+ ions can travel across the membrane to the F-side, forming LiF salt. The Standard Potentials add, for a total voltage of 5.9V. Remember, this is the energy that is imparted per Coulomb of electrons flowing through this direct current circuit.
Lithium Fluoride would be one of the highest voltage electrochemical cells possible, with a Standard Potential of 5.9V, because lithium is one of the strongest reducing agents and fluorine is one of the strongest oxidizing agents. Wikipedia maintains a useful list of Standard Potentials.
Charging a battery is simply running this same circuit in reverse. Likewise, electrowinning is an electrical technology used to separate metals from mixtures, such as aluminium, zinc, copper, silver and gold. There are even attempts to electrowin steel. Green hydrogen is the electrochemical product of electrowinning water. For all of these systems, the required Voltage can be computed from the Standard Potentials of the redox pairs (our own attempt to do this is here).
The Nernst Equation for Open Circuit Voltage?
Actual voltage in an electrochemical cell differs from Standard Potential, according to reaction conditions, temperature and molar concentrations. These deviations are captured by the Nernst Equation.
The Nernst Equation approximates the energy potential (in Volts) of an electrochemical reaction, based on the reagents, their concentrations, their temperature and other constants. It was formulated by the German Chemist, Walther Nernst (1864-1941), who is also partly credited with formulating the third law of thermodynamics.
The Nernst Equation states that the Reaction Potential E = E0 – (RT/nF) lnQ. To unpack these variables:
Eo is the Standard Potential for the redox reaction between reagents.
R is the Universal Gas Constant of 8.314 (J/mol-K), in turn the product of the Boltzmann Constant (J/K) and Avogadro’s Constant (particles/mol).
T is the absolute temperature in Kelvin.
n is the number of electrons transferred in the redox reaction (e.g., 1 for Li -> Li+ + e-).
F is Faraday’s Constant (Coulombs/mol), in turn the product of the elementary charge of an electron (C) and Avogadro’s Constant (particles/mol).
Q is the ratio of concentrations between reagents in the reaction. Q is going to change over time, as reagents are consumed. Q is going to vary, in particular, in a battery, according to its state of charge.
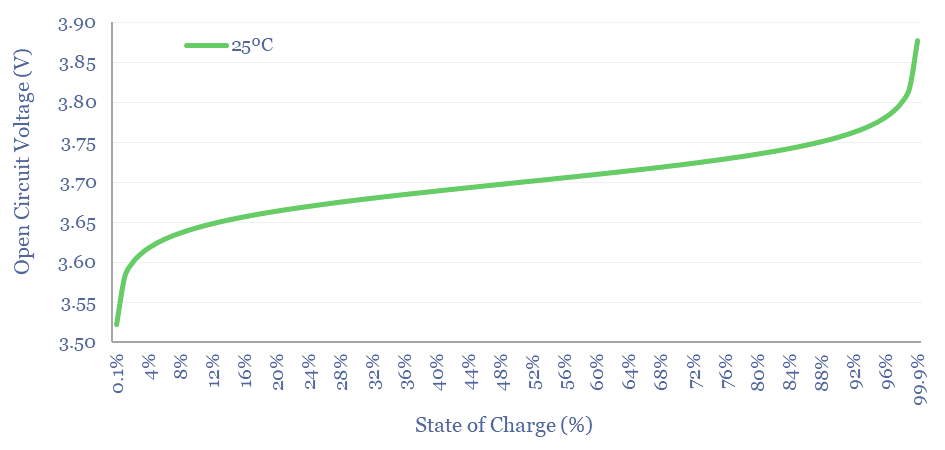
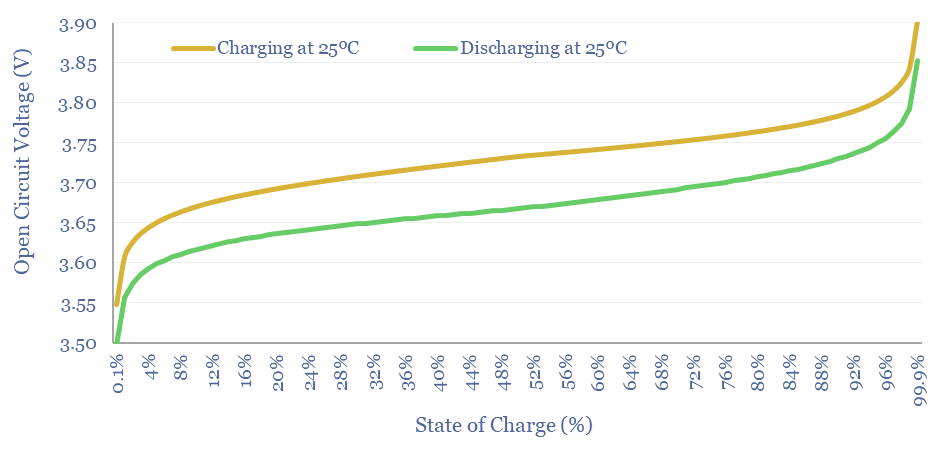
How does lithium ion battery voltage vary with State of Charge?
We have used the Nernst Equation, in the chart above, to capture a lithium ion battery with a 3.7V Standard Potential.
Cell Voltage matches Standard Potential when the concentration of Li+ in solution matches the concentration of Li intercalated at the anode. Here [LiC6] = [LiMxOy]. Hence [LiMxOy]/[LiC6] = 1. Hence ln(1) = 0. Hence E = E0.
As the battery is discharged, most of the MxOy sites at the cathode have already been occupied at the cathode, and there is very little LiC6 left to dissociate at the anode. Hence the [LiMxOy]/[LiC6] term in the Nernst Equation becomes very large. Hence the Voltage of the Battery falls. Since Power = Voltage x Current, and Voltage is dropping, it would be necessary to flow faster currents to sustain the same power output. This is why users sometimes report batteries “running out quite suddenly”.
The cutoff voltage for a lithium ion battery is around 3V. Battery degradation occurs when lithium ion batteries are over-discharged, such as dissolution of the copper current collector at the anode.
As the battery is charged, most of the LiC6 sites have already been occupied at the anode, and there is little LiMxOy left to dissociate at the cathode. Hence the [LiMxOy]/[LiC6] term in the Nernst Equation becomes very small. Note than when x is less than 1, ln(x) is negative. Hence the Voltage needed to continue charging the battery rises.
Higher voltages can chemically break down other materials in the battery and also contribute to battery degradation. For example, the standard potential for decomposition LiPF6 electrolyte is just over 5V. Hence there is an inherent trade-off, where cells with higher Voltage will tend to be more energy dense, but also more degradation-prone.
Why do batteries degrade faster at higher temperatures?
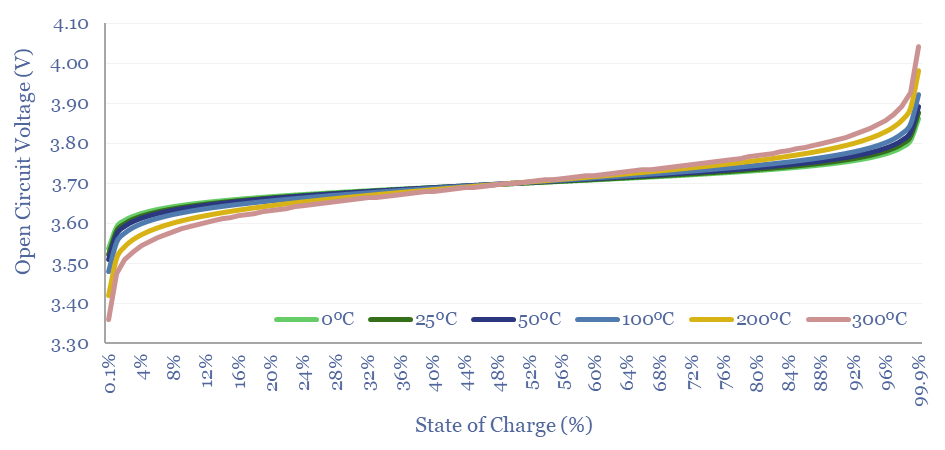
The Nernst Equation helps to explain why batteries degrade faster at higher temperatures. It features absolute temperature as an input variable.
With higher temperatures, voltage variations become more extreme, for both high charges and extreme discharges (chart below).
Other chemical side-reactions will also be promoted at higher temperatures via the Boltzmann Equations. Especially if there are hotspots in the battery during charging.
Does battery hysteresis impact efficiency?
When an electrochemical cell is charged, or discharged, the electrode materials become polarized. Polarizing the electrodes consumes a voltage. Resistance within the cell also causes a voltage drop. And there is usually an overpotential at the electrodes of any electrochemical cell. Hence the voltage needed to charge a cell is usually higher than the voltage measured when discharging it. These losses are relatively small, around 1-3%.
Other losses include Ohmic losses (from resistance), Coulombic losses (from chemical side-reactions and shunt currents) and System losses (e.g., from any battery management system, inverters, converters or other power electronics). But overall, the round-trip efficiency of a lithium ion battery should be around 85-90%.
Other real world issues?
The Nernst Equation gives a useful framework for understanding the voltage of electrochemical cells. Real world batteries have additional complexities, which can cause voltage curves to deviate. Electrodes are crystalline solids. The compositions, size and structure of these materials can impact Li/Li+ potentials. There can even be quite abrupt changes in Voltage, where the intercalation ‘reorganizes’ the crystal structure of cathode materials (e.g., from cubic spinel to tetragonal spinel).
The download linked below contains the maths and data behind the charts in the article. For other battery-related data-files, please see our broader research into batteries.
