The density of gases matters in turbines, compressors, for energy transport and energy storage. Hence this data-file models the density of gases from first principles, using the Ideal Gas Equations and the Clausius-Clapeyron Equation. High energy density is shown for methane, less so for hydrogen and ammonia. CO2, nitrogen, argon and water are also captured.
The Ideal Gas Law states that PV = nRT, where P is pressure in Pascals, V is volume in m3, n is the number of mols, R is the Universal Gas Constant (in J/mol-K) and T is absolute temperature in Kelvin.
The Density of a Gas can be calculated as a function of pressure and temperature, simply by re-arranging the Ideal Gas Law, where Density ρ = P x Molecular Weight / RT. Our favored units are in kg/m3.
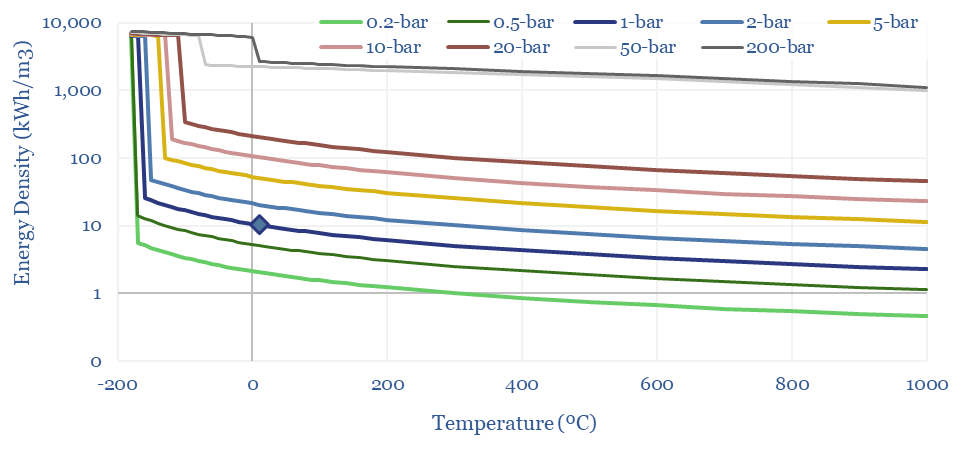
Density of methane in kg/m3 and kWh/m3
The Density of Methane (natural gas) can thus be derived from first principles in the chart below, using a molar mass of 16 g/mol, and then flexing the temperature and pressure. This shows how methane at 1 bar of pressure and 20ºC has a density of 0.67 kg/m3. LNG at -163ºC is 625x denser at 422 kg/m3. And CNG at 200-bar has a density of 180kg/m3.
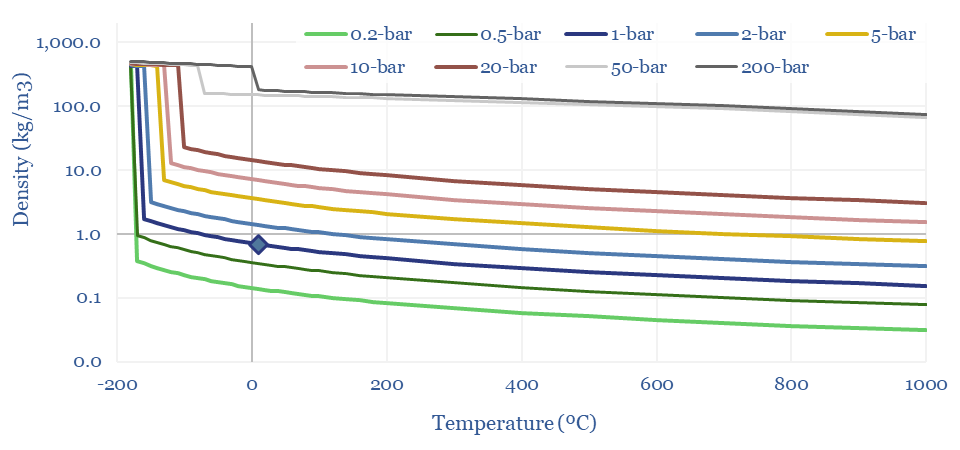
The Energy Density of Methane can thus be calculated by multiplying the density (in kg/m3) by the enthalpy of combustion in kJ/kg, and then juggling the energy units. A nice round number: the primary energy density of methane is 10 kWh/m3 at 1-bar and 20ºC, increasing with compression and liquefaction. CNG at 200-300 bar has around 30-60% of the energy density of gasoline, in kWh/m3 terms.
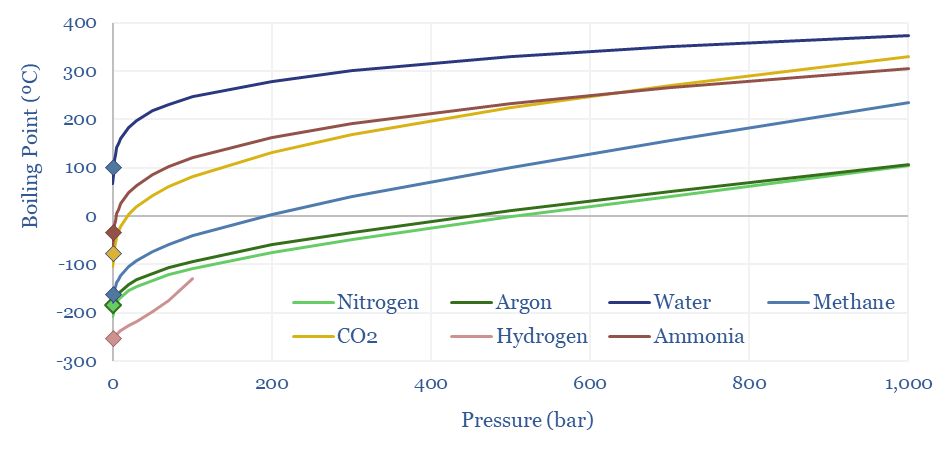
Clausius-Clapeyron: gas liquefaction?
Methane liquefies into LNG at -162ºC under 1-bar of pressure. The boiling points of other gases range from water at 100ºC, ammonia at -33ºC, CO2 at -78ºC, argon at -186ºC, nitrogen at -196ºC to hydrogen at -259ºC. This is all at 1-bar of pressure.
However, liquefaction temperatures rise with pressure, as can be derived from the Clausius-Clapeyron equation, and shown in the chart below. At 10-20 bar of pressure, you can liquefy methane into ‘pressurized LNG’ at just -105 – 123ºC, which can sometimes improve the efficiency of LNG transport. This can also help cryogenic air separation.
Density of CO2: strange properties?
The Density of CO2 is 1.87 kg/m3 at 20ºC and 1-bar of pressure, which is 45% denser than air (chart below). But CO2 is a strange gas. It cannot exist as a liquid below 5.2 bar of pressure, sublimating directly to a solid. CO2 can also be liquefied purely by compression, with a boiling point of 20-80ºC at 30-100 bar of pressure.
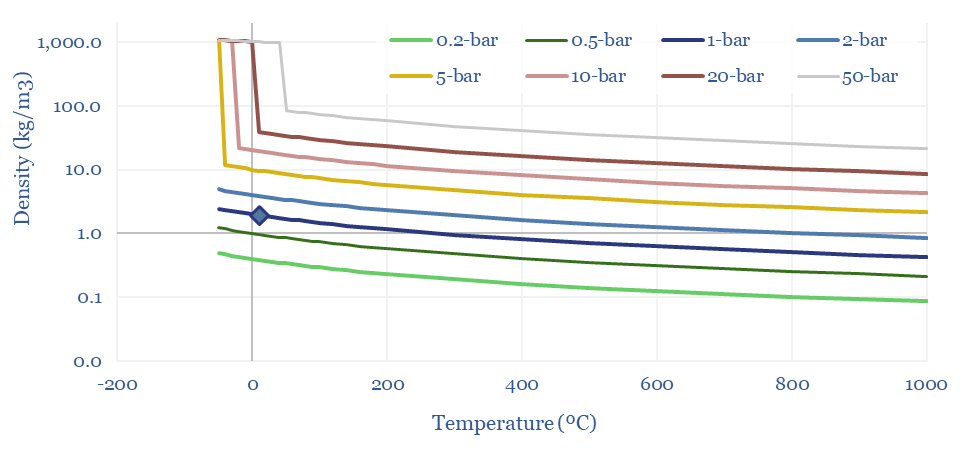
Hence often the disposal pipeline in a CCS or blue hydrogen value chain may often be pumping a liquid, rather than flowing a gas. And finally, these properties of CO2 open the door to surprisingly low cost CO2 transport by truck or in ships. This is all just physics.
Super-critical fluids: fourth state of matter?
There is also a fourth density state for all of the gases in the data-file. Above their critical temperature and critical pressure, fluids ‘become super-critical’. Sometimes this is described as ‘having properties like both a gas and liquid’. Mathematically, it means density starts rising more rapidly than would be predicted by the Ideal Gas Equations.
Super-critical gases behave unpredictably. Their thermodynamic parameters cannot be derived from simple formulae, but rather need to be read from data-tables and/or tested experimentally. This is why the engineering of supercritical systems tends to involve supercomputers.
Examples of super-critical gases? Steam becomes supercritical above 218-bar and 374ºC. CO2 becomes supercritical about 73-bar and 32ºC. Thus CO2 power cycles inevitably endure supercriticality.
Energy density of hydrogen lags other fuels?
The Density of Hydrogen is 0.08 kg/m3 at 20ºC and 1-bar of pressure, which is very low, mainly because of H2’s low molar mass of just 2g/mol. Methane, for example, is 8x denser. CO2 is 20x denser. In energy terms, gasoline is 3,000x denser per m3.
Hence hydrogen transportation and storage requires demanding compression or liquefaction. Tanks of a hydrogen vehicle might have a very high pressure of 700-bar, to reach a 40kg/m3 (the same density can be achieved by compressing methane to just 50-bar!). Liquefied hydrogen has a density around 70kg/m3 (LNG is 6x denser).
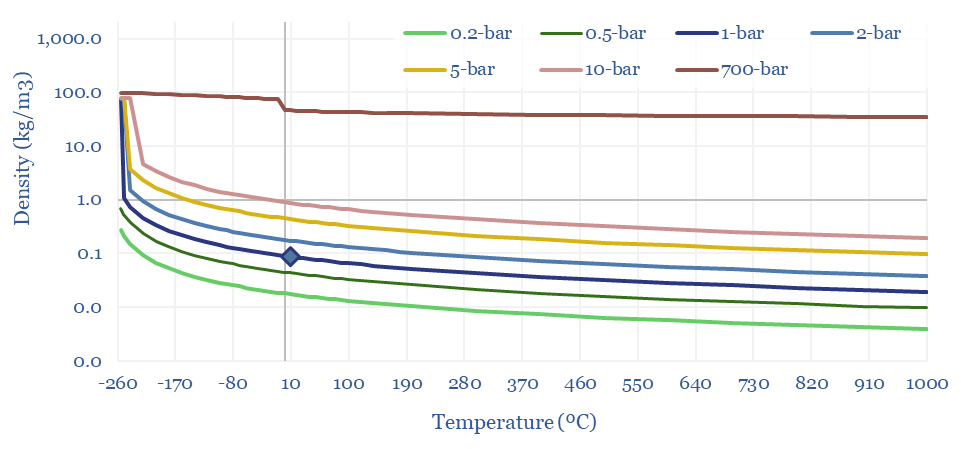
The energy density of hydrogen, in kWh/m3 also follows from these equations. At 1-bar and 20ºC, methane contains 3x more energy per m3 than hydrogen. Under cryogenic conditions, it contains 2x more energy. Under super-critical and ultra-compressed conditions, it contains 4x more.
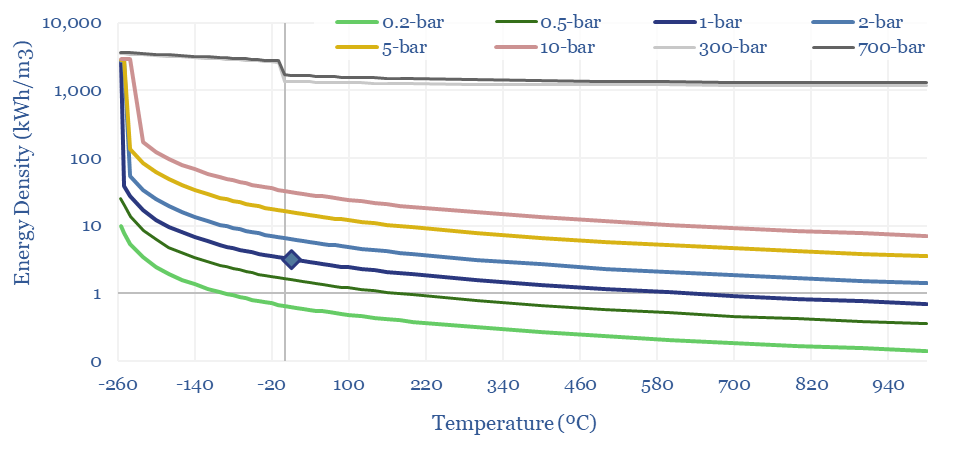
Data into the energy density of gases?
Similar energy density challenges constrain the use of ammonia as a fuel, as tabulated in the data-file, contrasted with other fuels, and discussed in our research note here.
This data-file allows density charts — in kg/m3 and in kWh/m3 — to be calculated for any gas, using the Ideal Gas Laws and the Clausius-Clapeyron equations. The data-file currently includes methane, CO2, nitrogen, ammonia, argon, water and hydrogen.