The Boltzmann constant, denoted as kB, or 1.381 x 10^-23 J/K, is the most important number in thermodynamics. It denotes the rate at which a single particle will gain thermal energy (in Joules) as its absolute temperature rises (in Kelvin). It underpins the Boltzmann distribution and the Maxwell-Boltzmann distributions, which matter in modelling gases, energy flows, efficiency, chemical processes and semiconductors.
The Boltzmann constant, denoted as kB, or 1.381 x 10^-23 J/K, is the most important number in all of thermodynamics. It denotes the rate at which a single particle will gain thermal energy (in Joules) as its absolute temperature rises above absolute zero (in Kelvin).
The Boltzmann constant was named (by Max Planck) after the Austrian scientist, Ludwig Boltzmann (1844-1906). Boltzmann was the first physicist to define entropy, as S = kB x ln(Ω), where kB is our eponymous constant and Ω is the number of micro-states available to the system (for more, see our overview of thermodynamics).
The Boltzmann constant in gas equations?
Universal gas laws? In an idealized gas, pressure (in Pascals) x volume (in m3) = number of molecules x absolute temperature (in Kelvin) x the Boltzmann constant (in Joules/Kelvin).
We find ourselves using these physics when modelling gas turbines, compressors, cryogenics, industrial gases, LNG, CCS, hydrogen.
Boltzmann in chemistry and materials?
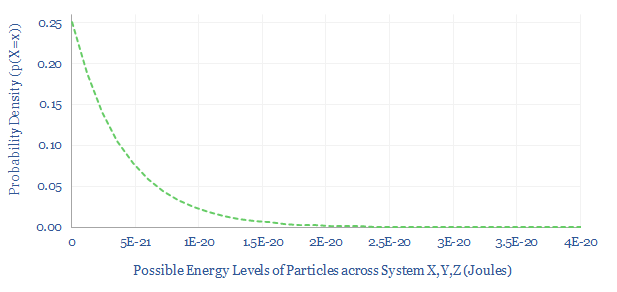
The Boltzmann expression? Maths using the Boltzmann constant often feature the expression exp(-E/kB.T). Here, exp denotes the natural exponent (e to the power x), E is the energy level, kB is the Boltzmann constant and T is absolute temperature. To give a sense, this expression is plotted below. As energy increases, exp(-E/kB.T) decreases. Or in other words, in a hotter system, some particles have dramatically more energy.
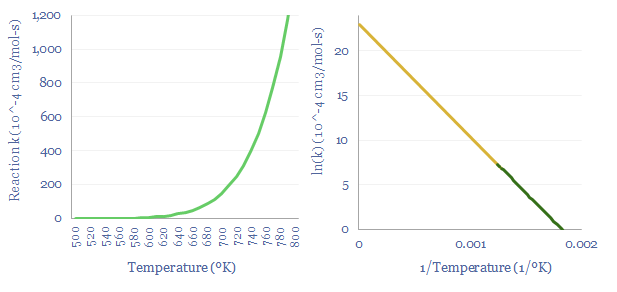
Chemical reactions are governed by the Boltzmann expression. The Arrhenius Equation states that reaction rates are a constant function of exp(-Ea/kB.T), where Ea is the activation energy (in kJ/mol). The left hand chart below shows that chemical reactions proceed exponentially faster when temperatures are higher, which is why industrial heating is over 25% of all global energy use. Faster reactions will tend to occur in hotter thermodynamic systems.
Carbon removal applications? Nature based solutions are low-cost and help nature, but they are also slow. CCS and DAC are much faster at absorbing CO2, but the very reason they work faster is that more energy is being injected into these reactions. If we want to accelerate CO2 removals, we need more nature and/or to cure energy shortages.
Boltzmann distributions maximize entropy?
Boltzmann distributions. The reason that higher temperature accelerates chemical reactions exponentially is that particles in a system will tend to have different energy levels. These energy levels fall on a statistical distribution. And as temperatures rise, dramatically more particles will have energy levels above the activation energy. Let us unpack some of this in the following paragraphs.
How are the energy levels of particles distributed in a thermodynamic system? Answer: in the configuration that maximizes the overall entropy of the system, thereby honoring the Second Law of Thermodynamics (entropy increases in a closed system).
What distribution of energies maximizes system entropy? If you started out with N particles in a 3D space (X, Y, Z), each with the exact same energy level of ‘E’, then over time, the particles would begin bumping into each other, exchanging momentum at each collision (some particles gain energy, some particles lose energy). Ultimately the system would ‘settle’ along a distribution of energy across X, Y, Z that maximized the overall entropy. You can model this in a computer simulation. Or you can do some fiendish calculus involving Lagrange multipliers. But the statistical distribution you will end up with is the Boltzmann Distribution.
The Boltzmann distribution is the distribution of energy levels of particles across a 3D system (X, Y, Z) that maximizes the total entropy of the system. Its Probability Density Function (PDF) contains our old friend, exp(-E/kB.T), as shown in the chart below.
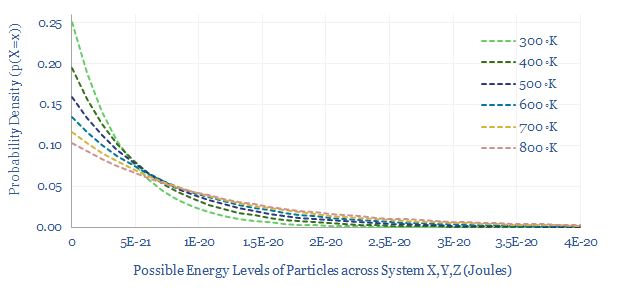
When temperature increases, more particles can occupy higher energy levels. For example, note that when temperature increases from 300K to 400K, the average particle has 40% more energy, but the number of particles with >2 x 10^-20 Joules of energy rises by 3.5x. This is why higher temperatures increase reaction rates exponentially.
Maxwell-Boltzmann Distribution of Velocity?
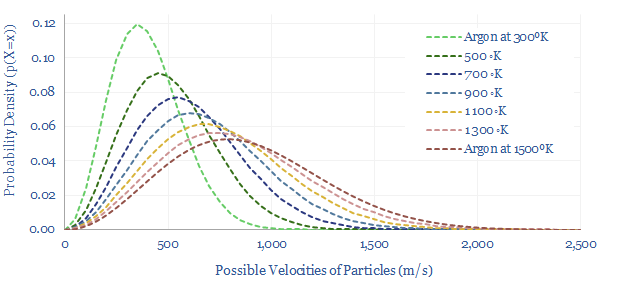
Another variant is the Maxwell-Boltzmann distribution shown below. Here, the maths have been adjusted, in two main ways. First, the x-axis shows the velocity of particles, rather than their energy levels (they are related though, as Kinetic Energy = 0.5 x mass x velocity^2). Second, the equation no longer cares about the locations of particles in space (X, Y, Z), but rather, looks across the overall system.
The Maxwell-Boltzmann distribution shows the most likely (i.e., entropy-maximizing) distribution of particle velocities across an entire system. Again, higher temperatures will dramatically increase the number of particles at high velocities and energy levels.
The real world, new energies and beyond?
Why does water evaporate below its boiling point? Water boils at 100C (overview here). Yet a puddle will evaporate without ever rising above its ambient temperature. Again this can be explained by Boltzmann equations. In order to evaporate, a single liquid particle must reach a critical ‘escape velocity’, or in other words, its energy level must surpass the latent heat of vaporization for water, which is 40.7 kJ/mol (or 6.8 x 10^-20 per water molecule). This same principle is also used in manufacturing lithium ion batteries, where solvents (such as NMP) must be evaporated below their boiling point, because their boiling points are high enough to degrade binders/additives in the electrodes.
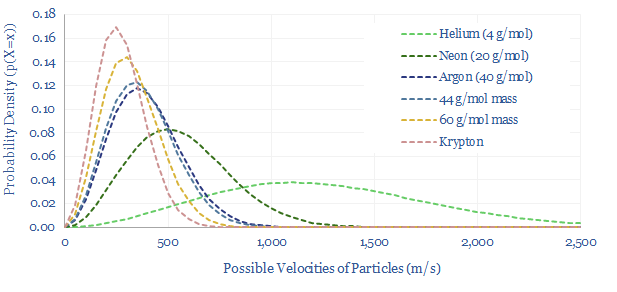
Maxwell-Boltzmann equations in practice. Modelling the rate of water evaporation or other real-world systems becomes annoyingly complex, because these systems are ‘degenerate’. In the chart above, we plotted Argon, which is a mono-atomic inert gas. Below, along similar lines, we can plot helium, neon and krypton, noting that more massive particles hold more of their momentum in mass, less in velocity. But we cannot simply plot di-atomic gases or more complex molecules. In addition to holding energy as kinetic energy, each bond in these gases can rotate, expand/contract and vibrate. In other words, at any given particle velocity, there are multiple energy levels available to the particle, which is known as degeneracy, and makes the maths more complicated.
Finally, in semiconductors, such as solar cells, Boltzmann’s constant feeds into the Fermi-Dirac distribution, which gives the probability of a possible energy level above (or below) the bandgap being occupied by an electron (or hole). This probability rises with temperature, and gets multiplied by the degeneracy of that energy level to yield the density of charge carriers. The formula for conductivity is the density of charge carriers x the charge per charge carrier x the mobility of charge carriers in the material. You can probably tell from the previous sentences that the maths here are somewhat complicated.
The purpose of this data-file is simply to give some worked examples of the Boltzmann distribution, Maxwell-Boltzmann distribution and the Arrhenius equations, applying these different probability distributions in practice. Please download the data-file to explore the maths.