The thermodynamic efficiency of materials production averages 20%, within an interquartile range of 5% to 50%. In other words, if the thermodynamic minimum energy needed to make a typical material is 1,500 kWh/ton, then the most likely case is that a typical industrial process for that material today consumes 7,500 kWh/ton of energy.
This note explores the numbers and implications. Calculations are linked here. The work makes us more optimistic on the potential for efficiency gains as part of the energy transition, especially in complex value chains, forms of CO2 capture, and using AI.
Definitions: what is thermodynamic minimum energy for materials?
ΔHf° denotes the Standard Enthalpy of Formation. This is the change of enthalpy (i.e., heat), when 1 mole of a substance forms from its constituent elements in their reference state.
For example, the chemical element silicon will slowly oxidize when exposed to air, yielding pure white sand (Si + O2 -> SiO2). Now for some numbers. This reaction involves a release of enthalpy, of -910 kJ/mol. The molar mass of silicon is 28.1 grams/mol. Hence by division, the energy released per mol of silicon is 32kJ/gram, which, by juggling the energy units, equates to 9,000 kWh/ton. If you walked along the most pristine beach in the world, with some kind of “magic ray gun” that decomposed SiO2 back into Si and O2, then the thermodynamic minimum energy needed is going to be the same number, around 9,000 kWh/ton, to overcome the enthalpy of formation of SiO2. In reality, there actually is a broad landscape of silica producers, who mine high-purity silica, and sell this product on, into value chains that yield glass, solar panels and semiconductors. For the latter two applications, silica might be reduced into silicon ‘metal’ in an electric arc furnace. And overall, we think this industrial process requires around 13,500 kWh/ton of input energy. Or in other words, producing low-purity silicon metal is about 67% efficient.
Hence in our analysis, we can compare the Standard Enthalpy of Formation with the actual industrial energy consumption of producing different materials.
If you want to calculate some of these standard enthalpies of formation yourselves, there are excellent free reference sources online, such as Engineering Toolbox.
Methodology: getting the right baseline?
Other examples are more complex than our silicon study above, and require some careful consideration of the appropriate baseline.
We don’t want to ‘cheat’ in our numbers by starting from some unrealistic baseline (“if I have a working iPhone, right here in my hand, then the energy costs of making an iPhone are zero”).
Ammonia makes a nice example. The standard enthalpy of formation of ammonia (NH3) is -46 kJ/mol. This is an exothermic reaction, releasing 750 kWh/ton of energy. But clearly the global ammonia industry is a net energy consumer, not a net energy producer!!
Remember, the standard enthalpy of formation assumes you are forming ammonia from its constituent elements, i.e., gaseous hydrogen and gaseous nitrogen.
Pure hydrogen does not occur naturally, but itself needs to be produced, most likely by steam methane reforming.
And pure nitrogen does not occur naturally: it needs to be separated out of air, overcoming the entropy of mixing, using air separation technology.
So in our analysis, our thermodynamic minimum (i) adds the minimum thermodynamic work to separate pure nitrogen from air (ii) adds the minimum thermodynamic work to decompose a 50/50 mixture of CH4 and H2O into pure hydrogen (iii) subtracts the energy that could theoretically be harnessed as the nitrogen and hydrogen react together again.
The result is that we think the minimum thermodynamic efficiency for producing ammonia is something around 1,200 kWh/ton. Compared to this baseline, the real-world ammonia industry is typically around 12% efficient.
The point here is that in each case, in our data-file, we need to make some ballpark estimates about what is a fair starting point, and it is from this baseline that the minimum thermodynamic work is calculated.
Conclusion #1: high thermodynamic efficiencies are challenging to achieve in the real world?
The average material in our screen has a c20% thermodynamic efficiency. In other words, real world industrial processes tend to consume around 4-5x more energy than the thermodynamic minimum (chart below), even after 100-200 years of incremental efficiency gains by industrial civilization.
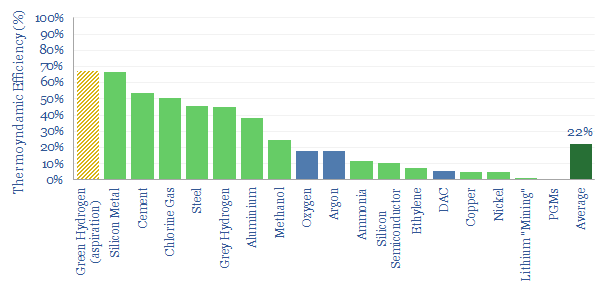
Conclusion #2. Complex value chains tend to be less efficient?
For the bottom quartile of processes in our data-file, the thermodynamic efficiency is below 5%. In other words, real world industrial processes tend to consume over 20x more energy than the thermodynamic minimum. Generally, these appear to be more complex value chains, starting with less concentrated input materials, and demanding more sophisticated output materials.
Another illustration of this point is that the very simple ‘silicon metal’ example, which we discussed above, yields one of the highest efficiencies. So too does thermally decomposing CaCO3 in cement production, or thermally reducing Fe2O3 in iron ore reduction for steel. On the other hand, the industrial processes needed to produce battery materials, lithium, nickel, PGMs are an order of magnitude more complex.
Conclusion #3. Efficiency Opportunities?
There are enormous opportunities in industrial efficiency. If we had run the charts above and found that most materials value chains were already in the mid-90s efficiency levels, then there would not be much opportunity for future improvement. But half of all the materials value chains in the world are around 20% efficient and one-quarter are less than 5% efficient.
This matters as energy efficiency is one of the most important controversies in the future of global energy demand and in the energy transition (notes below). Especially given that human civilization produces over 60 bn tons per year of ‘stuff’ across 40 different material categories, accounting for 40% of all global energy use and 35% of all global emissions.
Conclusion #4: beware hydrogen hubris?
One of the more surprising bars in our charts is over green hydrogen, where many forecasters are hoping that future value chains will be around two-thirds efficient (build-up here). It is simply interesting to note that this assumption would make hydrogen an outlier on our thermodynamic efficiency chart.
To re-iterate, if it were possible to convert two-thirds of ratable incoming electricity into useful recoverable hydrogen energy, then this would be one of the most efficient materials value chains in all of global industry.
It should be noted, we think, that the Gibbs Free Energy of hydrogen is 237 kJ/mol, while the Enthalpy of Formation is 286kJ/mol, and so there is always going to be a 13% energy loss in trying to recover useful energy back out of hydrogen as an energy carrier.
We would be wary of some studies that quote efficiency relative to the Gibbs Free Energy baseline, rather than the enthalpy baseline. This will tend to overstate efficiency. Being 100% efficient relative to the Gibbs Free Energy baseline still connotes a 13% loss relative to the enthalpy baseline.
Another very interesting point is that in thermodynamic terms, it is materially easier to make hydrogen from reforming methane than from electrolysing water. Methane is 25% hydrogen by mass, while water is 11% hydrogen. While the enthalpy of formation of methane from C and H is -75kJ/mol, the enthalpy of formation of water from H and O is -286kJ/mol. In other words, it takes 3.8x more energy to decompose H2O than CH4, and the decomposition of H2O yields 50% less H2 than the decomposition of CH4. Some might see this as an argument for making hydrogen out of CH4 rather than out of H2O, for example, in blue hydrogen or turquoise hydrogen value chains (more below).
Conclusion #5: still looking for magic bullets in CCS and DAC?
If you are starting from a baseline of air, with 400ppm CO2 concentration (i.e., 0.04%), then the minimum thermodynamic energy needed to separate out CO2 can be calculated via the Entropy of Mixing, and comes out at 134kWh/ton (calculation here). If energy costs 10c/kWh, this is $13/ton. This is not a high energy use or a high energy cost.
The challenge today is that technically ready DAC processes are only around 5% efficient (model here), and even many technically ready CCS applications absorb 10-50% of the energy that was harnessed when emitting that CO2 in the first place (note here).
There is going to be potential for CCS and DAC in the future of materials science. We have screened some of these opportunities, and will continue screening them in our CCS research, but for now, the two notes below capture what we are looking for, to get excited by next-gen membranes and adsorbents.